La matemática Ester Dalvit tiene en este momento un contrato postdoctoral INdAM-Marie Curie en el Departamento de Matemáticas de la Universidad de Toronto; las trenzas a las que se refiere el título no tienen nada que ver con el cabello de Ester… se trata de un concepto matemático.
Con motivo de su tesis New proposals for the popularization of braid theory, Ester Dalvit realizó en 2012 la película titulada A journey through the mathematical theory of braids, en el que de manera amena explica la teoría matemática de trenzas.

La película está dividida en cuatro partes, cada una de las cuales dura unos 15 minutos. Está pensada para estudiantes y profesorado de los últimos años de secundaria, pero sobre todo para los primeros años de universidad. En opinión de Ester, también es accesible para el público en general, que no debe preocuparse por no entender todo el contenido, pero que puede aprender algunas cuestiones matemáticas y dejarse fascinar por los aspectos más complejos de la teoría de trenzas (ver [4]).
Los capítulos están concebidos para verlos en orden; los dos primeros son sencillos y los dos últimos son más complejos conceptualmente, aunque la parte visual que los acompaña es también más completa. Se describe a continuación el contenido de cada uno de ellos:
- La estructura de grupo. Se dan las definiciones de trenza, de grupo de trenzas y se finaliza dando la presentación de Emil Artin (1925) que aún hoy en día es la más conocida y utilizada.
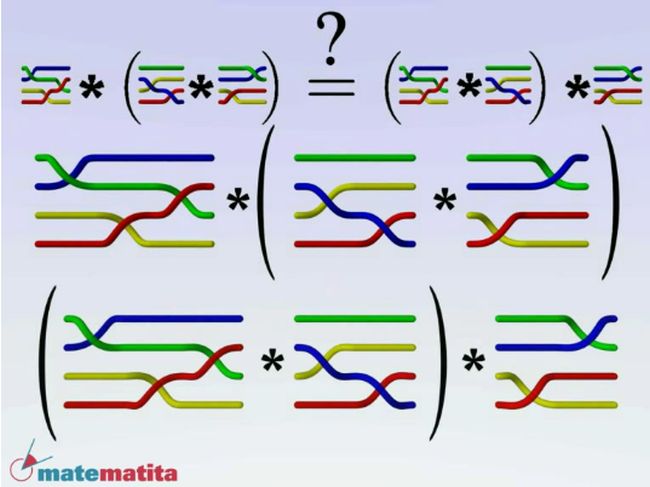
- El problema de las palabras. Se trata uno de los problemas clásicos de la tepría combinatoria de grupos: dadas dos palabras en los grupos de trenzas, ¿cuándo representan la misma trenza? Se presentan algunos algoritmos, uno debido al propio Artin y otro de Patrick Dehornoy.

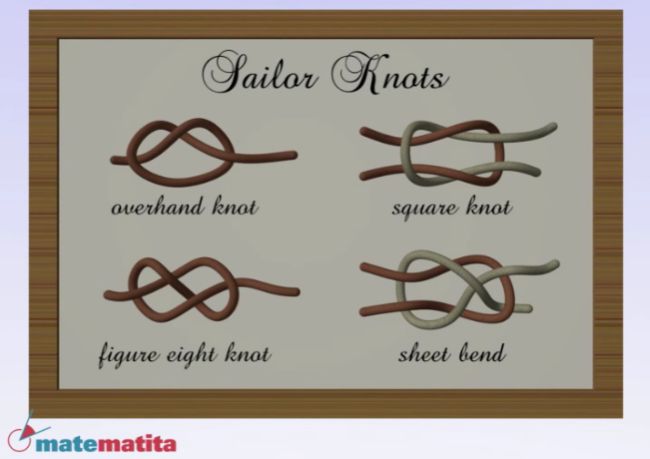
- Incursión en la teoría de nudos. Los nudos son objetos topológicos muy próximos a las trenzas. Se presenta el polinomio de Jones, que es un invariante de un nudo y que puede definirse a partir de las trenzas.
- Danzas de Hilden. Se describen las trenzas como movimientos (danzas) de puntos en el disco. Se presenta un subgrupo especial del grupo de trenzas y se describe otra relación entre trenzas y nudos diferente del dado en el capítulo 3.

La película se ha realizado principalmente con POV-Ray (Persistence of Vision Ray-tracer), un programa de raytracing gratuito.
Debajo se incluyen los cuatro capítulos en inglés, aunque en A journey through the mathematical theory of braids pueden verse también en versión italiana y francesa.
Más información
- Ester Dalvit, A journey through the mathematical theory of braids, University of Trento, matematita, 2012
- Página de Ester Dalvit, Universidad de Trento
- Página de Ester Dalvit, Universidad de Toronto
- Aurélien Alvarez, Tresses en mouvement, Images des Mathématiques, CNRS, 2 de agosto de 2014
- Marta Macho Stadler, Trenzando y bailando, ::ZTFNews, 2 de agosto de 2014
Sobre la autora
Marta Macho Stadler es doctora en matemáticas, profesora del Departamento de Matemáticas de la UPV/EHU y colaboradora en ::ZTFNews y la Cátedra de Cultura Científica de la UPV/EHU.