María Teresa Lozano Imízcoz: ‘Poner en común ideas siempre multiplica las soluciones’

María Teresa Lozano Imízcoz es licenciada (1969) y doctora en matemáticas (1974) por la Universidad de Zaragoza y Honorary Fellow de la Universidad de Wisconsin (EE.UU., 1976-1978). Desde 1978 es profesora de la Facultad de Ciencias de la Universidad de Zaragoza, donde desarrolla su labor docente e investigadora. Catedrática de Geometría y Topología desde 1990, es Académica Numeraria de la Real Academia de Ciencias Exactas, Físicas, Químicas y Naturales de Zaragoza desde 1996. Además, es Académica Correspondiente de la Real Academia de Ciencias Exactas, Físicas y Naturales desde 2006.

Coincidí con María Teresa Lozano Imízcoz en el XXI Encuentro de Topología –reunión informal de matemáticas y matemáticos vinculados a la Red Española de Topología– que tiene lugar una vez al año. Conversamos sobre el trabajo que realiza una especialista en esta área de conocimiento.

Marta Macho Stadler (Marta): ¿Recuerdas cuando empezó tu gusto por las matemáticas? A veces se nos olvida cómo empezó ese interés…

María Teresa Lozano Imízcoz (María Teresa): No lo recuerdo muy bien. Desde pequeña tuve facilidad para las materias de ciencias, y me gustaba la geometría y la física. Lo cierto es que mi primera intención era estudiar la carrera de Físicas (si conseguía una beca para poder ir a Zaragoza o a Madrid) o estudiar alguna carrera de ciencias en Pamplona donde yo vivía. Pero la Primera Olimpiada Matemática me premió con una beca para estudiar la carrera de Matemáticas, y eso fue determinante. Después vino todo rodado (aunque no sin esfuerzo, constancia y apoyo familiar para superar las dificultades): la licenciatura, la tesis doctoral, la estancia posdoctoral en Madison (USA) y el puesto en la Universidad de Zaragoza.

Marta: Tu trabajo de investigación se enmarca en el área de la topología. La gente a veces confunde la topología con la topografía –incluso recuerdo un encuentro de topología en el que en la entrada del restaurante universitario en el que comimos, el cartel que nos indicaba el camino decía “Encuentro de tocólogos”–. ¿Podrías decirnos en pocas palabras qué es para ti esta rama?

María Teresa: Se dice que la Topología es la rama de las Matemáticas que se ocupa de caracterizar algunas propiedades cualitativas de los objetos, aquellas que permanecen tras una deformación continua sin roturas ni pegados. Es algo así como una geometría blanda. Su creador fue Henri Poincaré, aunque él no le puso este nombre. Estas ideas solo pudieron surgir en una mente privilegiada con una extraordinaria capacidad de abstracción espacial como la suya.

Marta: ¿A qué te dedicas dentro de la topología?

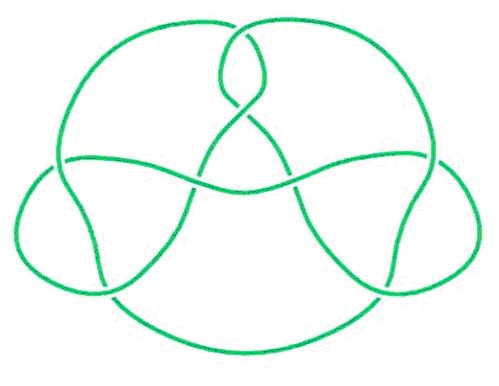
María Teresa: Me interesa la geometría y la topología de objetos de tres dimensiones. Es decir de los espacios que localmente son como el mundo en que vivimos, con tres grados de libertad. Como localmente todos estos espacios son iguales, interesa conocer las propiedades globales, cómo es el objeto, que forma tiene, y también que geometría puede admitir en su interior,… También me interesa la Teoría de nudos, aunque más bien como herramienta para trabajar en dimensión 3. Un nudo matemático responde a la imagen real de una cuerda anudada con sus extremos identificados. Es en realidad una manera de meter la circunferencia en el espacio. Ocurren por ejemplo como órbitas o trayectorias cerradas de un objeto puntual. Su clasificación no es sencilla. No es fácil averiguar si puedes convertir un nudo en otro sin cortar ni pegar la cuerda cerrada.

Marta: Nudos… esto parece más bien cosas de magos o de marineros. Muchas veces se “nos reprocha” a las personas que hacemos matemática teórica de estar “fuera de la realidad”. ¿Se aplican tus matemáticas a la vida real?

María Teresa: Sí claro, como vivimos en un mundo tridimensional donde tienen lugar todos los fenómenos físicos, todo el conocimiento que podamos alcanzar de este ambiente es utilizable a corto o largo plazo. Te recuerdo algunos ejemplos: La Teoría de nudos, sirve para la clasificación cualitativa de flujos atendiendo al tipo de nudos que aparecen como trayectorias cerradas; El estudio de la geometría de nuestro universo y la existencia de singularidades ayuda a entender su evolución; también hemos visto en este Encuentro de Topología la aplicación de técnicas topológicas a reconocimiento de imágenes en medicina.

Marta: Es verdad, una conferencia bien bonita.

María Teresa: Por otra parte hay una aplicación lúdica que pocas personas conocen y que tiene importancia cultural: La influencia de las figuras geométricas y topológicas en insignes artistas plásticos. Algunos ejemplos: Los relojes blandos de Dalí son deformaciones topológicas de relojes reales; las esculturas de los hermanos Antoine Pevsner y Naum Gabo, pertenecientes al constructivismo ruso de la primera mitad del siglo XX, fueron inspiradas en figuras didácticas de superficies construidas por los alumnos de Felix Klein y Alexander Brill en la Universidad Politécnica de Munich a finales del siglo XIX, donde ellos estudiaron; la geometría hiperbólica inspiró la obra de M.C. Escher…

Marta: ¡Qué interesante! No conocía todas estas influencias. ¿Crees que al igual que la pintura y la escultura se nutren de la geometría y la topología, el mundo de las matemáticas podría de alguna manera inspirarse en las artes plásticas?

María Teresa: Bueno, más que inspirarse yo diría que comparte con las artes plásticas una búsqueda de la belleza, aunque esta esté en segundo lugar. Creo que la matemática creativa que introduce nuevos conceptos abstractos para estudiarlos metódicamente lo hace buscando de algún modo la belleza en las construcciones y los resultados. Lo mismo hacemos cuando buscamos una buena demostración. Queremos que sea elegante, sencilla, bonita. ¿No has oído a veces decir a un matemático con entusiasmo: “¡Esta demostración (o esta teoría) es preciosa!”?

Marta: Sí, es que hay matemáticas realmente preciosas…

María Teresa: Yo creo que un buen matemático debe pensar como un arquitecto: Lo importante es que un edificio (una teoría) sirva para cumplir su cometido, pero si además se consigue una obra de arte, mucho mejor.
Fíjate, un ejemplo muy sencillo: hay demostraciones gráficas del teorema de Pitágoras que son una maravilla.

Marta: Es verdad… ¿Estás especialmente orgullosa de alguno de tus resultados?

María Teresa: Es difícil destacar unos resultados sobre otros pero voy a citarte dos: uno por ser el más conocido y otro por ser el último. Además tú, como topóloga, me puedes perdonar que el lenguaje sea un poco técnico.
Creo que el resultado más conocido lo obtuve en colaboración con H. Hilden, J.M. Montesinos y W. Whitten, y se refiere a la universalidad de un enlace conocido como Los anillos de Borromeo. (Se llama así porque fue utilizado en el emblema heráldico de la familia Borromeo, y son tres circunferencias enlazadas de manera que si una se corta las otras dos se separan). El resultado dice, a grosso modo, que toda variedad tridimensional se puede construir a partir del complemento de Los anillos de Borromeo, esto implica que cada variedad tridimensional cerrada y orientable está formada por un número finito de dodecaedros hiperbólicos pegados convenientemente por sus caras.

Últimamente hemos encontrado (con J.M. Montesinos) una familia de transiciones entre geometrías tridimensionales utilizando el concepto algebraico de cuaterniones, que nos permite estudiar completamente las estructuras geométricas de ciertas variedades cónicas singulares asociadas a nudos.

Marta: Vaya, parece bastante complejo… Veo que te has referido a trabajos en colaboración con otras personas. ¿Prefieres trabajar sola o en colaboración con alguien?

María Teresa: No hay duda de que es mucho más gratificante y productivo trabajar con otros investigadores. Cuando tienes alguna idea novedosa puedes comunicarlo y discutirlo, y con frecuencia sucede que tratando de explicar con claridad tu problema encuentras tu misma una solución en la que no hubieras pensado si no lo verbalizas. Poner en común ideas siempre multiplica las soluciones, porque no todos tenemos las mismas facultades y conocimientos. Pero esto no solo sucede entre matemáticos con los mismos intereses científicos, sabes muy bien que los avances más importantes se han hecho cuando se han puesto a trabajar juntos investigadores de distintos campos. Las matemáticas, y la ciencia en general, no deben de estar empaquetadas en compartimentos estancos. Por eso creo que son importantes los congresos, específicos y generales. Nos ponen en contacto con nuevas ideas y personas.

Marta: Es cierto, las fronteras entre disciplinas son cada vez más difusas. ¿Se necesita mucha intuición o visión espacial para hacer tus matemáticas?

María Teresa: En mi campo la visión espacial ayuda bastante, pero esta es una cualidad que se puede mejorar con la práctica. Hoy en día hay instructivos juguetes didácticos y programas informáticos que dibujan en tres dimensiones y permiten mover las imágenes. Debemos usarlos en las aulas y talleres, porque son divertidos y ayudan a formar la mente.

Marta: A veces se dice que la visión geométrica de los hombres está mejor desarrollada. ¿Estás de acuerdo?

María Teresa: Es verdad que algunas personas tienen más facilidad que otras para ver e imaginar figuras en el espacio, pero no creo que eso tenga que ver con el género. En el hipotético caso de que tuviera una base genética en los cromosomas X,Y, que no creo, la educación debería borrar esa diferencia.
Las diferencias de aptitudes mentales suelen tener que ver más bien con la educación y con la cultura de un lugar. Los trabajos que normalmente se realizan para este tipo de estudios son de tipo estadístico y hay que analizar bien la muestra que se utiliza. Los resultados con una muestra de un país y cultura no sirven para otro país con otra cultura. Estoy convencida que si a toda la población adulta de un lugar hacemos creer que las mujeres no tienen cualidades para la música (por ejemplo), esto se cumplirá en la siguiente generación, porque ninguna familia va a potenciar la música en sus hijas. Afortunadamente la cultura mediterránea ha potenciado más las matemáticas entre las mujeres que otras culturas. (Tradicionalmente las cuentas en casa las han llevado las mujeres, y el coser, hacer ganchillo y tricotar fomenta la visión espacial. Cito estas manualidades porque son algunas de mis viejas aficiones.)

Marta: También me dediqué al punto cuando mis sobrinos eran pequeños… ¿Crees que la ciencia básica no está de moda? ¿O es que no sirve para nada?

María Teresa: En principio la ciencia básica no tiene aparentemente aplicación inmediata y hoy en día queremos tener soluciones rápidas, por eso quizás no está suficientemente valorada. Pero las matemáticas en concreto están en la base de todos los avances tecnológicos y sin potenciar su investigación no conseguiremos más desarrollo. Quizás no está de moda, pero es nuestra misión conseguir que sea más valorada.

Marta: Las cosas no están muy fáciles hoy en día para la gente joven, ¿les animarías a hacer una tesis en un tema centrado en la topología? ¿O crees que lo tienen más fácil en una rama más aplicada?

María Teresa: Cuando un matemático decide continuar por el camino de la investigación haciendo una tesis doctoral, ya tiene sus preferencias. En ese momento nosotros les debemos ayudar en lo que sea necesario, pero es él el que tiene que valorar que quiere conseguir en el futuro, porque desgraciadamente no podemos asegurarles una carrera investigadora profesional segura. Eso sí, si disfruta con lo que hace será más feliz.

Marta: ¿Aconsejarías a tu gente joven cercana que estudiara matemáticas en este momento?

María Teresa: Si le gusta, claro que sí. Siempre van a ser necesarios los matemáticos, y se encontrarán con salidas profesionales cada vez más diversas, porque, como sabes, los estudios de matemáticas forman la mente dando más capacidad de análisis, síntesis y desarrollo, y eso se puede aplicar en muchos campos.

Marta: Muchas gracias por tu tiempo y tu amabilidad. Nos vemos prontito, de nuevo, en Zaragoza.

Sobre la autora

Marta Macho Stadler es doctora en matemáticas, profesora del Departamento de Matemáticas de la UPV/EHU y colaboradora en ::ZTFNews y la Cátedra de Cultura Científica de la UPV/EHU.