La historia de Margarete Hilbert me recuerda un poco a la del viejo ciclista francés Raymond Poulidor, conocido como el “eterno segundón”, por quedar siempre detrás del legendario Eddy Merckx o de Jacques Anquetil. Es muy probable que Margarete jamás subiera a una bicicleta profesional, ni tampoco alcanzó la fama del ciclista francés (Margarete no obtuvo fama en absoluto), pero en ambos casos sus figuras se vieron eclipsadas por otra mayor. En el caso de Margarete, el astro ensombrecedor fue su propio hermano, y el vacío bibliográfico en que cayeron sus logros es un ejemplo del comprensible olvido que sufren los familiares de celebridades, a excepción de singularidades donde el talento y el éxito son compartidos, como en las parejas de hermanos Chudnovsky o Bernouilli en las matemáticas, el caso de Pierre y Marie Curie en la física, o la familia Pelayo en su periplo estadístico por los casinos.
No lo tuvo fácil Margarete si acaso buscaba algún tipo de reconocimiento, aunque no parece que fuera así. Su hermano fue el célebre matemático David Hilbert, uno de los más prolíficos e influyentes de la historia: publicó innovaciones en múltiples ámbitos de la matemática, y en el año 1900 elaboró una lista con los veintitrés problemas más importantes pendientes de resolver, una compilación que sirvió de guía para la investigación matemática de gran parte del siglo XX. Pero no solo fue la abrumadora excelencia de la carrera de su hermano lo que ha impedido que el legado de Margarete sea conocido. Ser mujer ha representado, desde hace demasiados siglos, la más injustificada desventaja que la sociedad actual ha engendrado, un yugo que afecta a la práctica totalidad de los ámbitos, por supuesto también al de la ciencia, y del que solo hoy en día hay signos de estar despertando, no digamos a principios del siglo XX.
Por unos azares y estímulos que no considero adecuado relatar aquí, en un viaje que hice a Alemania, en otoño del 2012, tuve ocasión de visitar el fondo reservado de la biblioteca de la Universidad de Göttingen, una de las más prestigiosas del mundo. En sus facultades estudiaron o enseñaron más de cuarenta premios Nobel, y fue donde Hilbert ejerció cátedra hasta que se retiró. Gracias a los contactos y a la mano izquierda de mi amiga Katja Von Kleist, ambos tuvimos la oportunidad de hojear la tesis doctoral que publicó en el año 1885, y fue así como supimos de la existencia de su hermana Margarete. Concretamente, su nombre aparecía en una misteriosa nota que más bien parecía accidental o recordatoria, un garabato relegado a una esquina del margen derecho de la página sesenta y tres, al más puro estilo de Pierre de Fermat. Después de no pocos esfuerzos de desencriptación caligráfica, Katja concluyó que podía leerse: “consultar con Margarete”, una anotación que nos dejó primero intrigados, pero después impacientes por investigar.
Pasaron meses sin que ninguno de los dos fuera capaz de encontrar nada relacionado con Margarete. Lo más lógico era deducir de ello que la nota carecía de valor, pero a Katja y a mí nos parecía que, en un ámbito tan prolijo en publicaciones e historiadores, era cuanto menos curioso que no existieran menciones, y su figura fue entonces objeto de múltiples fabulaciones que compartíamos en una correspondencia intencionadamente literaria, como dos buscadores más preocupados por fantasear con las virtudes de un tesoro que por llevar su búsqueda hasta el final. Por desgracia las pesquisas resultaban siempre infructuosas, y del mismo modo en que lo hacen las relaciones a distancia, la intensidad y creatividad de nuestras ocurrencias se fueron difuminando, y según mi bandeja de entrada, la última conversación electrónica se produjo el día 6 de junio de 2013. A partir de entonces nuestra relación se limitó a eventuales “like” en redes sociales, pero no habíamos vuelto a conversar telemáticamente hasta que, el 29 de diciembre del pasado 2017 (es decir, según la fecha en la que estoy escribiendo esto, hace apenas dos meses), recibí un whatsapp suyo. Me sorprendió que eligiera ese medio (siempre hablábamos por correo electrónico), pero aún me sorprendió más el contenido de su mensaje. Decía: “No te lo vas a creer. ¿Te acuerdas de Margarete Hilbert? He tenido acceso a unas cartas que se escribieron ella y su hermano entre los años 1932 y 37, las tengo todas digitalizadas, cuando puedas ponte en contacto conmigo, tienes que leerlas, no tienen desperdicio”.
En un primer momento, no cupe en mi asombro. Descubrir, casi cuatro años después, que de algún modo nuestra imaginación y sospechas habían acertado, fue una sorpresa arrebatadora, y sentí renacer de inmediato la vieja pasión que nos produjo el personaje de Margarete. El descubrimiento merecía un reencuentro, y a las pocas horas ya había comprado un billete de vuelo para Alemania. Después de llegar a su apartamento en el barrio de Neukölln, en el centro de Berlín, y después de las cordialidades y de las rápidas puestas al día, Katja me dio una traducción al castellano de todas las cartas que había conseguido, en una sobreactuada y memorable ceremonia de la que guardo divertidas fotografías. Aquella noche, mientras cenábamos y después bebíamos cerveza, Katja me contó por encima el contenido de las cartas, pero no fue hasta regresar a mi casa, tres días después, cuando las pude leer con tranquilidad. Descubrí entonces que la relación entre los dos hermanos, por lo menos en su expresión epistolar, no rezumaba en absoluto desigualdad intelectual. Los años en los que las cartas estaban escritas eran los últimos de la carrera de Hilbert, pero los temas matemáticos eran frecuentes, y en el discurso de Margarete se percibe un nivel de conocimientos universitarios, seguramente también matemáticos. En la carta del 9 de setiembre de 1935, por ejemplo, Margarete le escribe a David (según la traducción de Katja): “Considero que vas a llevarte un chasco con tu último proyecto en teoría de la demostración. Pretendes dotar al edificio de la lógica de un alcance absoluto, pero estoy segura de que alguien lo va a derrumbar”. Dos semanas después, David le respondía: “Hermana, tus virtudes adivinas o intuitivas no dejarán de sorprenderme. Estás en lo cierto: Kurt Gödel ha echado por tierra mis aspiraciones con dos teoremas tan brillantes como fulminantes”.
Pero las cartas no son exclusivamente matemáticas. A través de su lectura supe que Margarete había emigrado a los Estados Unidos, y que vivía, desde el año 1926, en el distrito de Harlem, en Nueva York. De algunos comentarios se deduce que su vida sentimental fue más bien tormentosa, y en más de una ocasión escribe sobre un tal Francis con una ternura que hace pensar que se trató de un hijo suyo, quizá desaparecido o lejos de ella. El personaje de Margarete aparece como una figura con mucha seguridad en sí misma, quizá una empresaria o funcionaria de rango –en cualquier caso una persona adinerada– y a menudo usa un tono maternal con David. Se detecta además un refinado sentido del humor, y es evidente que frecuentaba la vida nocturna de la ciudad.
Respecto al contenido matemático de las cartas de Margarete, la verdad es que no sé cómo clasificarlo. En sus reflexiones hay menciones a una gran variedad de temas, muy sospechosamente parecidos a aquellos en los que destacó su hermano David. Debido a esta concordancia, Katja defiende una postura un tanto extrema, según la cual el verdadero genio residía en la mente de Margarete, y David era solo una marioneta. En las cartas Margarete señala ideas que, por su tono, parece que le fueran propias (tanto en análisis funcional como en teoría de números), e incluso parece adivinarse una comunicación estable con George Cantor, coétano de la época y de cuyas ideas sobre el infinito David fue acérrimo defensor. De entre toda la correspondencia, el material que halló Katja debe ser solo una parte, puesto que a veces hay conversaciones que no tienen continuidad, pero en muchas ocasiones Margarete aconseja a David con una solvencia y autoridad que indican que, en efecto, “consultar con Margarete” era una práctica habitual. La teoría de Katja no es pues tan descabellada, y es posible que la de Margarete fuera una opinión de mucho valor para David, pero aunque el guión de la mujer a la sombra es atractivo y casi cinematográfico (era la fantasía preferida de Katja cuando aún no sabíamos nada de Margarete), su veracidad resulta difícil de sostener, no solo porque existen múltiples relatos sobre la brillantez personal de David, sino por la dificultad que supondría que fuera Margarete quien dirigiese, desde los Estados Unidos, el liderazgo que ejercía su hermano, desde Alemania, sobre la comunidad matemática internacional.
En mi opinión la figura de Margarete es una rareza iluminadora. A excepción de los ejemplos como los que ya he citado al principio (y de muchos otros actuales o anónimos), no es tan frecuente encontrar cooperaciones prolíficas entre hermanos. La idea de competición ha calado en profundidad en la sociedad y reside en la esencia del ser humano: se trata de una inercia biológica con una representación clara en la infancia, cuando los infantes pugnan por obtener la atención y el afecto de sus padres. Con todas sus complejidades y diversidades de caracteres, este patrón se reproduce de generación en generación, y el modelo actual de educación no ha conseguido, ni mucho menos, cambiar la tendencia. El camino a la popularización del trabajo en equipo, de la filosofía del diálogo y del entendimiento, y en última instancia del desvanecimiento del ego, es una de las asignaturas pendientes de nuestra sociedad, y en este sentido el ejemplo de los hermanos Hilbert es peculiar pero alentador; a pesar del lamentable machismo todavía imperante, y de la enorme sombra que ejercería sobre Margarete la carrera de David, por el tono de ambos se percibe que no había rivalidad alguna, y si uno lee sus cartas sin saber su autoría, en ciertos momentos se hace difícil saber quién es quién.
Margarete discutía con David sobre temas de actualidad científica, pero sus mejores ideas son de otro género, en cierto modo más extravagantes, aunque algunas pasarían por actuales. En la carta del 6 de febrero de 1934, por ejemplo, Margarete escribe: “David: matemáticas se escribe en femenino, sé que te cuesta reconocerlo, pero has de asumir que nos pertenecen, algún día el dominio del hombre llegará a su fin”. Su inclasificable lista de reflexiones discurre entre temas variopintos, y ni Katja ni yo hemos sido aún capaces de descifrarlas todas, pero Margarete relaciona las matemáticas con conceptos como el amor, la soledad, el complejo de Edipo y la nostalgia, y los fragmentos que sus propuestas generan no tienen nada que envidiarle a los del tipo más académico, pertenecientes a la esfera de David.
No voy a explicar aquí todo el material que tradujo Katja, pero si he decidido escribir este capítulo, es porque hay una idea que no puedo resistirme a desvelar. En su carta del 12 de mayo de 1936, durante un breve relato de su fin de semana, Margarete usa por primera vez la palabra “jam”, y añade entre paréntesis su significado. En la jerga del mundo del baile, una “jam” es una reunión social donde se baila música swing, un derivado del jazz. Como ya he dicho antes, Margarete frecuentaba los locales nocturnos de Harlem, luego no es extraño que asistiera, a finales de la década de los veinte, a la explosión de popularidad de la Savoy Ballroom, donde nacieron el swing y su baile asociado, conocido como “lindy-hop”. Margarete viviría en primera persona ese momento histórico, y no cabe duda de que sabía de la existencia de esas jams. La idea de Margarete aparece de manera intermitente en diferentes cartas, pero cristaliza en la del 20 de octubre de 1936, cuando se refiere a ella como la “Jam Infinita”.
Supongo que debo añadir en este punto que, si la idea en cuestión me parece tan irresistible, es porque yo mismo soy aficionado a bailar lindy-hop. Desde hace poco más de un año asisto a clases, y de vez en cuando también a las jams. Encontrar, en una carta fechada en el año 1936, la conjunción de dos de mis pasiones (las matemáticas y el swing) ha sido para mí un verdadero hallazgo. Es cierto que sus demás figuraciones son genuinas y sugerentes (aunque a veces también disparatadas o temerarias, cuando no irrealizables o sencillamente incomprensibles), pero, en mi opinión, el concepto de “jam infinita” representa el culmen de su creatividad. Es la menos práctica o realista, la de menos consecuencias o relevancia, pero es también la más original y fantástica, además de también la más paradójica, y quizá por eso sea la única de la que se tiene constancia más allá de las cartas.
Como decía antes, no queda claro si la propia Margarete bailaba swing, pero es evidente que conocía uno de los problemas que suelen producirse en las jams. El sistema en ellas está muy definido: los hombres (denominados “leaders”) lideran el baile marcando los pasos, ellas (las “followers”) completan las figuras y las embellecen, y las parejas se intercambian a cada canción. En la actualidad cada vez hay más mujeres que actúan de leaders, y también hombres que lo hacen de followers, pero en general se mantiene la tradición; si ya no es sencillo aprender uno de los roles, no digamos después aprender el otro. Lo habitual, pues, es que hagan falta un hombre y una mujer para bailar, pero tradicionalmente sucede que, en general, buena parte de los hombres encuentra más importantes o adecuados otro tipo de aficiones que quizá se le dan mejor o considera más viriles, y tiene menor tendencia a aficionarse al baile que la mujer. Esto suele producir situaciones de insuficiencia en cuanto a número de hombres, un desequilibrio que debió de preocupar a Margarete, porque lo compartió con David en una de sus cartas. De nuevo faltan algunas por completar la secuencia, pero en la que David le escribió a Margarete el día 29 de abril de 1937, aparece la frase que desencadena el prodigio. “Hermana, no pierdas la cabeza”, escribe David, “si en una jam hay el doble de mujeres que de hombres, siempre quedarán mujeres sin ningún hombre con el que bailar”.
La afirmación de David, de entrada, parece obvia, y resulta intrigante qué fue lo que dijo Margarete para provocarla. Si a una jam asisten cien mujeres y solo cincuenta hombres, está claro que habrá cincuenta mujeres que se quedarán sin pareja, y parece incuestionable que la conclusión continuará siendo cierta para cualquier número de hombres que asistan, si asisten también el doble de mujeres. La respuesta de Margarete, sin embargo, constituye el momento más álgido de todas sus cartas, y refuerza la hipótesis de que, o bien conocía personalmente a George Cantor, o bien su trabajo. Dice así: “Hermano, vuelves a ser incapaz de ver más allá. Olvidas el carácter finito de tus razonamientos, y por eso te pierdes a la verdad. Si la condición que pones es que haya el doble de mujeres que de hombres, he de decirte que existe un caso en el que, no solo toda mujer tendrá un hombre con quien bailar, sino que no quedará nadie sin bailar”.
A pesar de la evidente condescendencia de Margarete, quizá debida al descuido teórico de su hermano, la respuesta de David está exenta de acritud. “Hermana, vuelves a tener razón. Había olvidado que por fin es posible tratar con el infinito de tú a tú. En efecto, si a la jam se presentan infinitos hombres e infinitas mujeres, incluso habiendo dos mujeres por cada hombre, siempre será posible emparejarlos a todos. Basta con etiquetar a las mujeres con los números naturales” (el uno, el dos, el tres, etcétera), “numerar después a los hombres con los números pares” (el dos, el cuatro, el seis, etcétera), “y emparejar a cada mujer con el hombre cuyo número sea el doble del de ella”. En posteriores cartas el tema desaparece, pero en la última de las cartas de que dispongo, la del 28 de noviembre del 1937, hay un dibujo delicioso donde hay dos filas infinitas (simbolizadas con puntos suspensivos al final), y una serie de flechas que ilustran el procedimiento: la follower número uno bailará con el leader número dos, la dos con el cuatro, la tres con el seis, la cuatro con el ocho, y así sucesivamente, de manera que cada hombre tendrá una mujer asociada (basta dividir su número por dos para encontrarla) y cada mujer tendrá un hombre asociado (basta multiplicar su número por dos para encontrarlo), de manera que nadie queda desemparejado, y por lo tanto, a pesar de haber el doble de mujeres que de hombres, en realidad hay el mismo número, y nadie se queda sin bailar.
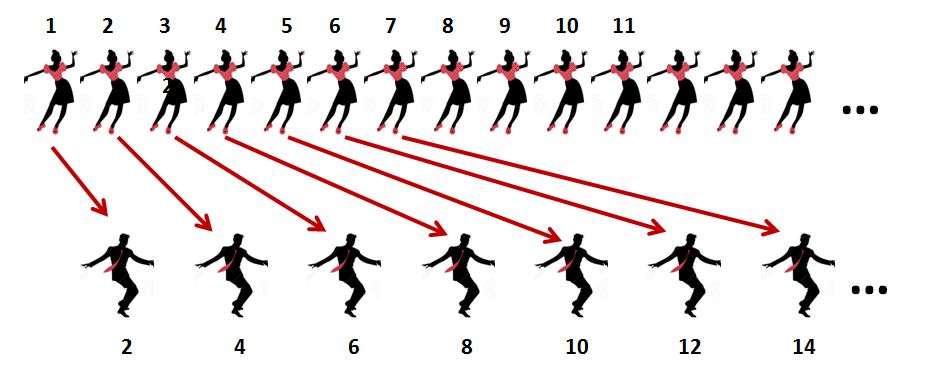
Que los dos hermanos apliquen herramientas de la teoría de los números transfinitos al contexto del swing me parece una gema de las conexiones matemáticas. La intuición sugiere que los números pares son la mitad de la totalidad de los números, pero el método de emparejamiento (una biyección, en nomenclatura matemática) demuestra que, cuando se cruza la frontera hacia lo infinito, las cosas no son lo que parecen. Con la misma técnica George Cantor demostró que hay tantos números enteros como naturales, tantas fracciones como números naturales, o tantos números (incluidos ahora los decimales) entre el cero y el uno que entre el cero y el dos, o que (repitiendo el razonamiento) entre el menos infinito y el más infinito. Estas paradojas no eran ninguna novedad para los dos hermanos, pero algo debió de comentar Margarete en su entorno, o algo debió de llegar a oídos de los organizadores de fiestas, porque, según el Harlem Journal (desaparecido en el año 1956), el 22 de mayo de 1939, la Savoy Ballroom celebró una fiesta con un cartel donde puede leerse: “Damas y caballeros, les presentamos la Jam Infinita, la jam donde ninguna mujer se quedará sin bailar”.
No hay constancia de cómo se produjo exactamente la fiesta, aunque es probable que la idea del infinito sobrevolara el evento, supongo también que con un componente de humor. En mis fantasías Margarete estaría en la puerta numerando a mujeres y a hombres, y les mostraría el funcionamiento de la biyección. Tampoco sé cómo salvarían el hecho de que, por muy multitudinaria que fuera la fiesta, es imposible que asistieran infinitas personas. Sin embargo, algo debió de suceder en aquella primera edición, porque un año y medio después, en otro local nocturno de la misma ciudad, hubo otro evento que volvió a llamarse “La Jam Infinita”, con un cartel casi calcado al anterior.
David murió en el año 1941, y su hermana Margarete en el 59. Por supuesto mi búsqueda dista mucho de ser exhaustiva, pero no he encontrado más pruebas de jams infinitas. Por otra parte, después de su popularidad el mundo del swing dejó paso a otras modas, de manera que el legado de Margarete parece haber muerto, disuelto en la espalda negra del tiempo. Quizá sea pues cierto que existan figuras que eclipsen a otras, y que Raymond Poulidor nunca será recordado como a Eddie Mercks o Jaques Anquetil. El tiempo aniquila personajes e ideas, y la historia oscurece a quien no brilló suficiente. Asumir que sus luces se apagan es comprender el flujo del tiempo, pero algo de mí se resiste a tirar la toalla, y considero que Margarete merece un esfuerzo. Quizá escribir esto ya fuera suficiente, y publicarlo contribuiría a su perdurabilidad. Sin embargo, después de más de cuatro años conviviendo con ella en nuestra imaginación, Katja y yo hemos decidido ir un poco más allá. Concretamente, aprovechando la popularidad que vive de nuevo el mundo del swing, hemos organizado una fiesta que, por supuesto, hemos llamado “La Jam Infinita”. No sabemos si vendrá la suficiente gente como para aproximarnos a la fantasía de Cantor, si seremos capaces de divulgar las matemáticas de la propuesta, o si nuestro intento de homenaje será efectivo. De momento, lo que hemos hecho es añadirle al cartel, debajo del título, la frase “Damas y caballeros, les presentamos la jam donde ninguna mujer se quedará sin bailar”, y justo debajo, en letras pequeñas pero visibles: “consultar con Margarete, con Margarete Hilbert”.
Nota
Si os ha interesado la vida de Margarete Hilbert, clicad en este enlace para saber más sobre ella.
Sobre el artículo original
El relato (de ficción) Consultar con Margarete se publicó en el blog Materatura de Xavi Roca el 3 de febrero de 2018.
Un especial agradecimiento al autor del artículo por permitir su reproducción en Mujeres con ciencia.
Sobre el autor
Xavi Roca es licenciado en Matemáticas (UB) y ejerce la docencia en un instituto público dese cundaria en Tarragona. Además de las matemáticas y su didáctica, otra de sus pasiones es la literatura. Publica periódicamente sus relatos matemáticos en la web Materatura.