La ecuación de Seager: adaptando la de Drake

El astrónomo Frank Drake (1930-2022), uno de los pioneros del proyecto S.E.T.I., propuso en 1961 la fórmula que lleva su nombre. Esta ecuación permite estimar el número de civilizaciones inteligentes con tecnología avanzada y susceptibles de estar presentes en nuestra galaxia.

La fórmula de Drake se basa en conocimientos que van desde la astrofísica hasta la biología, y es el producto:

N = E × F_P × N_E × F_L × F_I × F_C × L,

donde:

1. N es el número de civilizaciones inteligentes con tecnología avanzada en la Vía Láctea.
   
2. E es el número de estrellas en nuestra galaxia.
3. F_P es la fracción de esas estrellas con sistemas planetarios.
4. N_E es el número de planetas favorables a la vida por cada sistema planetario.
5. F_L es la fracción de esos planetas en los que se desarrolla vida.
6. F_Ies la parte de esos planetas en los que emergen seres inteligentes.
7. F_C es la porción de esos planetas en los que sus habitantes desarrollan la suficiente tecnología para comunicarse.
8. L es la duración de la vida de una civilización avanzada.

En la referencia [1] pueden encontrarse diferentes estimaciones de este número N, teniendo en cuenta diferentes variables.

La astrofísica Sara Seager (1971) propuso en 2013 una versión paralela a la ecuación de Drake para estimar, en su caso, el número de planetas potencialmente habitables en nuestra galaxia. En vez de pensar en señales de radio –es decir, en civilizaciones con tecnología avanzada– Seager adaptó esta ecuación para centrarse únicamente en la estimación de presencia de vida.

Su ecuación pretende realizar un cálculo probabilístico de la existencia de vida, centrándose en los gases que ésta produciría y que podrían acumularse en la atmósfera del planeta a niveles detectables por telescopios lejanos. La ecuación de Seager es:

N = E* × F_Q × F_HZ × F_O × F_L × F_S,

donde:

1. N es el número de planetas con signos detectables de vida.
2. E* es el número de estrellas observadas.
3. F_Q es la fracción de estrellas que están en una fase estable de su existencia.
4. F_HZ es la porción de estrellas con planetas rocosos en la zona habitable.
5. F_O es la parte de planetas que pueden observarse.
6. F_L es la fracción de los planetas que tienen vida.
7. F_S es la parte de esos planetas sobre los que la vida produce una marca detectable de gas.

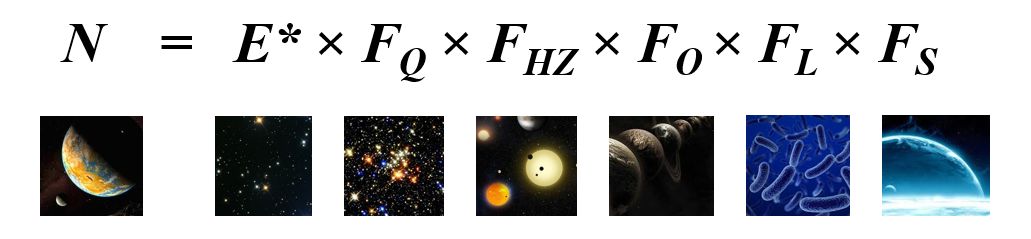
Seager introdujo valores para cada uno de estos términos (ver [2]), sugiriendo que podrían aparecer 2 planetas habitados durante la próxima década.

Más información

1. Ecuación de Drake, Wikipedia
2. Devin Powell, The Drake Equation Revisited: Interview with Planet Hunter Sara Seager, Space.com, 4 septiembre 2013
3. Sara Seager, An Equation to Estimate the Probability of Identifying an Inhabited World Within the Next Decade, 2013

Sobre la autora

Marta Macho Stadler es doctora en matemáticas, profesora del Departamento de Matemáticas de la UPV/EHU y colaboradora en ::ZTFNews y la Cátedra de Cultura Científica de la UPV/EHU.