Marjorie Rice: la pasión por resolver problemas matemáticos

Marjorie Jeuck nació el 16 de febrero de 1923 en San Petersburgo (Florida). Se crio en una pequeña granja cerca de Roseburg (Oregón). En esa ciudad aprendió en una sencilla escuela en la que algunos de sus maestros reconocieron su talento e incentivaron su incipiente interés por la ciencia.

Cuando Marjorie cursaba la enseñanza secundaria, su familia se mudó a Pine Castle (Florida). Allí estudió –sin demasiado éxito– taquigrafía y mecanografía y, para su disgusto, no pudo seguir ningún curso de matemáticas aparte del curso general exigido. Se graduó a los 16 años y, en 1945, tras trabajar en una lavandería y después en una imprenta, se casó con Gilbert Rice. Se mudaron a Washington, D.C. y más tarde a San Diego con su bebé. Este niño falleció, pero llegaron otros cinco y Marjorie se convirtió en madre y ama de casa a tiempo completo.

Marjorie nunca perdió su interés por las matemáticas. Ayudaba a su hijo mayor en sus tareas, encontrando en algunas ocasiones las soluciones a los problemas mediante procedimientos «poco ortodoxos». Frecuentaba la biblioteca pública buscando lectura científica e inculcó a sus hijos el interés por la ciencia.

La familia estaba suscrita a la revista Scientific American. Cuando Marjorie tenía un rato libre –cuando estaba sola en casa– leía con interés la columna Mathematical Games de Martin Gardner. En julio de 1975, Gardner describía en su sección de matemática recreativa ocho tipos de pentágonos convexos que teselaban el plano. Los últimos tres tipos habían sido descubiertos por el matemático Robert Kershner, quien había declarado que con ellos la clasificación de este tipo de teselaciones por pentágonos se había completado. Pero Kershner se equivocaba: en diciembre de 1975, Gardner anunciaba que el informático Richard James –uno de sus lectores– había descubierto un nuevo tipo de pentágono que embaldosaba el plano. La curiosidad de Marjorie se despertó y comenzó su propia investigación.

Sin conocimientos formales de geometría, pero con un agudo sentido de la organización, Marjorie desarrolló una notación propia para expresar las propiedades de los nueve tipos de teselaciones por losetas pentagonales conocidos hasta el momento. Representaba cada tipo de embaldosado mediante un pentágono en forma de casa, con líneas interiores indicando los ángulos en cada vértice del pentágono y sombreados identificando los lados iguales. En febrero de 1976, gracias a su metódica búsqueda, Marjorie encontró un nuevo tipo de pentágono teselando el plano y anunció su descubrimiento a Martin Gardner. Para comprobar que efectivamente ese pentágono era diferente de los nueve encontrados anteriormente, el divulgador envío las anotaciones de Rice a varias personas especialistas en la materia, entre ellas a la matemática Doris Schattschneider. Marjorie tenía razón, y Doris Schattschneider se convirtió en su contacto con la comunidad matemática (profesional).

Marjorie continuó sus búsquedas esporádicamente, encontrando y dibujando largas listas de pentágonos teselando el plano. Schattschneider le proporcionaba algunos artículos sobre teselaciones que animaban a Marjorie a emprender nuevas indagaciones. En diciembre de 1976, Rice encontró dos nuevos tipos de pentágonos teselando el plano y, en 1977 descubrió un nuevo tipo.

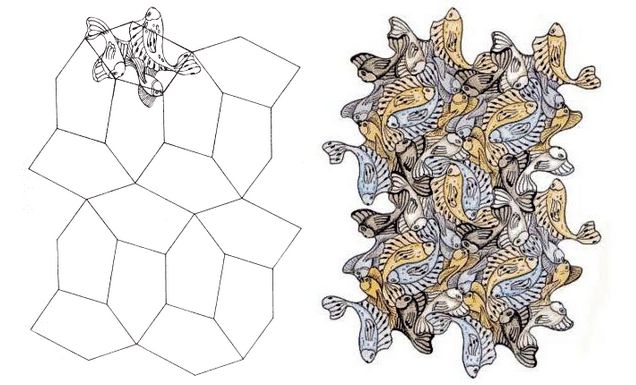
Los descubrimientos de Marjorie fueron una importante contribución al problema de caracterizar los pentágonos convexos que pueden teselar el plano. Pero también la inspiraron para realizar diseños decorativos similares a los de Maurits Cornelis Escher, adornados con flores, mariposas, abejas, conchas o peces.

Aunque no descubrió nuevos tipos de mosaicos por losetas pentagonales, Marjorie continuó durante muchos años aumentando sus listas y bocetos buscando completar la clasificación de teselaciones por pentágonos convexos. Doris Schattschneider seguía enviando a Rice artículos sobre el tema. Sin duda inspiraron a Marjorie, quien descubrió unas sesenta teselaciones diferentes con distintos tipos de pentágonos.

En 1999, uno de sus mosaicos se colocó –en forma de baldosas de cerámica esmaltada– en el vestíbulo de la sede de Asociación Matemática de América (MAA) en Washington, D. C.

En marzo de 1995, en una reunión de la MAA, Doris Schattschneider dictó una conferencia sobre el trabajo de Marjorie. La invitó a hablar ante la audiencia de especialistas en matemáticas. Marjorie no se atrevió a hacerlo, pero accedió a presentarse tras finalizar la conferencia de Schattschneider. Una calurosa ovación, con la audiencia en pie, agradeció el valor científico de su trabajo y la inspiración que representaba su esfuerzo.

En sus últimos años de vida Marjorie luchó contra el cáncer y la demencia senil. Esta última le llevó a olvidar tantos y tantos pentágonos que había estudiado con meticulosidad en el poco tiempo libre que le dejaba su familia. Falleció el 2 de julio de 2017, con 94 años.

Referencias

1. Doris Schattschneider, In praise of amateurs en The Mathematical Gardner, D. Klarner ed., Prindle, Weber & Schmidt, Boston, MA (1981) págs. 140-166
2. Doris Schattschneider, Marjorie Rice (16 February 1923–2 July 2017), Journal of Mathematics and the Arts 12 (1) (2017) 51-54
3. Natalie Wolchover, Marjorie Rice’s Secret Pentagons, Quanta Magazine, 11 julio 2017
4. Marta Macho Stadler, Teselando el plano con pentágonos, Cuaderno de Cultura Científica, 19 febrero 2020
5. Marjorie Rice, Intriguing Tessellations

Sobre la autora

Marta Macho Stadler es doctora en matemáticas, profesora del Departamento de Matemáticas de la UPV/EHU y colaboradora en ::ZTFNews y la Cátedra de Cultura Científica de la UPV/EHU.