Vera T. Sós, especialista en combinatoria

Vera T. Sós (1930) es una matemática húngara que ha trabajado fundamentalmente en teoría de números y combinatoria. Alumna de Lipót Fejér –como los célebres matemáticos Paul Erdős, George Pólya, Tibor Radó, Marcel Riesz o John von Neumann, entre otros–, colaboró activamente con Paul Erdős y Alfréd Rényi. Por supuesto, el número de Erdős de Vera T. Sós es 1; de hecho, publicaron treinta artículos juntos.

¿Y esa T. de su nombre? Corresponde a la primera letra de Turán, el apellido de su marido, Pál Turán (1910-1976), también alumno de Lipót Fejér y estrecho colaborador de Paul Erdős con el que trabajó durante cuarenta y seis años.

Vera Sós nació el 11 de septiembre de 1930. Tras graduarse, en 1948, conoció a Alfréd Rényi y Paul Erdős: colaboró más adelante con ellos gracias a su profesor, Tibor Gallai, que –según Vera Sós– fue la persona que descubrió su talento para las matemáticas. Estudió física y matemáticas en la Universidad Eötvös Loránd, graduándose en 1952. Conoció a Pál Turán en la universidad y se casaron en 1952; para él era su segundo matrimonio. El teorema de Kővári-Sós-Turán (ver 5.) es un trabajo conjunto del matrimonio con Tamás Kővári: en él proporcionaban una cota superior para la solución del problema de Zarankiewicz, una cuestión no resuelta en matemáticas que intenta averiguar cuál es el mayor número posible de aristas en un grafo bipartito que tiene un número dado de vértices y no posee subgrafos bipartitos completos de un tamaño dado.

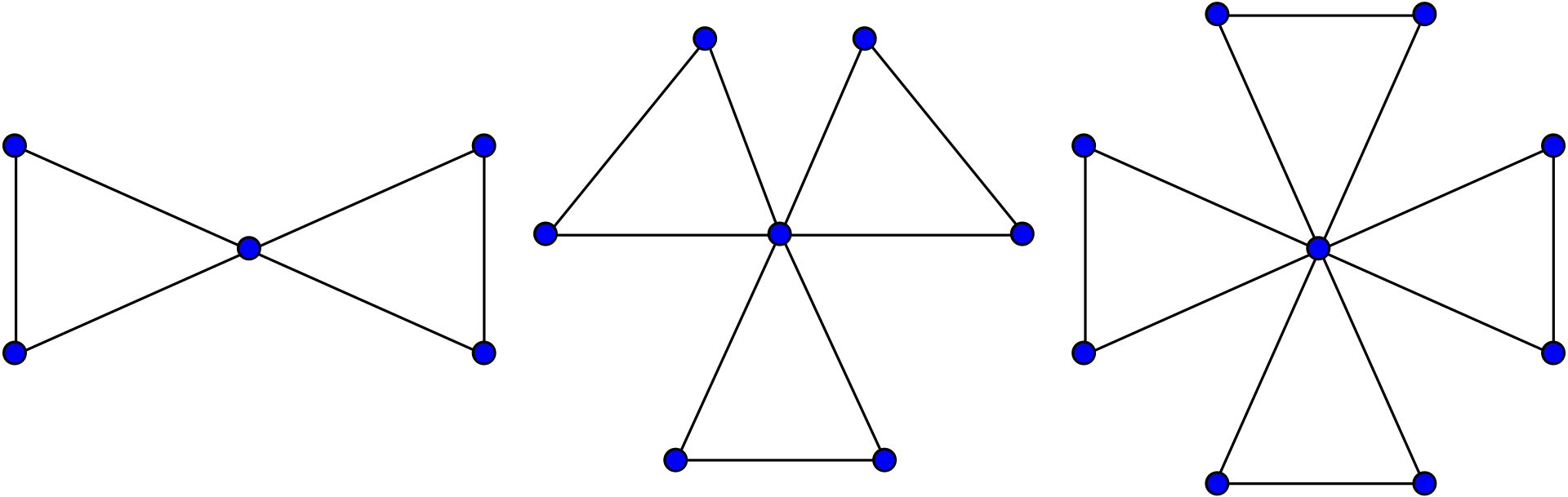
Otro de sus logros, esta vez junto a Paul Erdős y Alfréd Rényi, es el llamado teorema de la amistad. Este resultado afirma que los grafos finitos con la propiedad de que dos vértices cualesquiera tienen exactamente un vértice vecino en común son precisamente los grafos de la amistad (aquellos en los que un vértice está unido a todos los demás por una arista). Estos últimos grafos, denotados por F_n, son grafos planos y poseen 2n+1 vértices y 3n aristas.

Una manera de pensar en este teorema –y de allí su nombre– es el siguiente: si un grupo de personas posee la característica de que cada par de ellos tiene exactamente un amigo en común, entonces debe de haber una persona que sea amiga de todas los demás. Esta propiedad no es cierta para grafos infinitos.

En la década de 1950, Vera Sós demostró el teorema de tres distancias, resultado de teoría de números conjeturado por Hugo Steinhaus y demostrado independientemente por el matemático Stanisław Świerczkowski. Este teorema afirma que si se colocan n puntos en una circunferencia, en los ángulos de θ, 2θ, 3θ, etc. desde el punto de partida, habrá como máximo tres distancias distintas entre pares de puntos adyacentes alrededor de la circunferencia. Además, cuando hay tres distancias, la mayor de las tres siempre es igual a la suma de las otras dos. Y si θ no es un múltiplo racional de π, también habrá al menos dos distancias distintas.

Este teorema se aplica en ámbitos muy variados, como en el estudio del crecimiento de plantas, en los sistemas de afinación musical o en la teoría matemática de las palabras de Sturmian.

En 1965, junto a su compañero András Hajnal, Vera inició el seminario semanal Hajnal-Sós en la Sección de Matemáticas de la Academia Húngara de Ciencias. Este seminario se consideraba un «foro para nuevos resultados en la combinatoria» y sigue organizándose hoy en día.

Vera T. Sós ha sido distinguida con numerosos premios como resultado de su trabajo en matemáticas. Uno ellos es el prestigioso Premio Széchenyi –nombrado en honor al político y escritor István Széchenyi–, que recibió en 1997, que se otorga a aquellas personas que han realizado importantes contribuciones a la vida académica de Hungría.

Nota

Vera Turán Sós falleció el 22 de marzo de 2023.

Referencias

1. Vera T. Sós, Mathematics Genealogy Project
2. Vera Sós, Academia Europaea
3. Vera Sós, Simon Foundation, 2016
4. Vera Sós, Research Gate
5. Tamás Kővári, Vera T. Sós, Pál Turán, On a problem of K. Zarankiewicz, Colloquium Math., 3 (1954) 50-57
6. Wikipedia (castellano e inglés), consultadas el 6 abril 2019

Sobre la autora

Marta Macho Stadler es doctora en matemáticas, profesora del Departamento de Matemáticas de la UPV/EHU y colaboradora en ::ZTFNews y la Cátedra de Cultura Científica de la UPV/EHU.