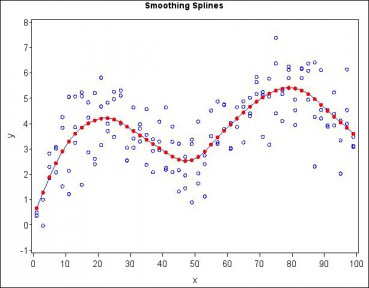
En las últimas décadas, el avance de las técnicas no paramétricas, mediante el uso de los métodos de suavizado para extraer la señal en datos con ruido, permite multitud de aplicaciones científicas. Uno de los métodos más habituales requiere el uso de los llamados smoothing splines, splines suavizados o simplemente splines. Brevemente, podemos decir que la estimación mediante un spline es una generalización de la estimación paramétrica. En el caso de una estimación paramétrica, el análisis estadístico clásico nos permite aproximar una curva (recta, cuadrática, etc.), mediante la estimación de aquellos parámetros que minimizan algún tipo de distancia. Así, los métodos de regresión simple obtienen los parámetros a y b que minimizan la suma de los cuadrados de di, definidos según la siguiente figura:
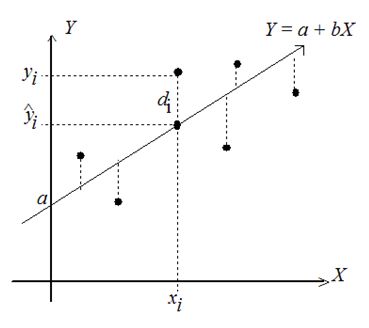En el caso de un spline, no hay una curva predeterminada y el único requisito es cierto grado de suavidad, regulado por el llamado parámetro de suavizado. Una vez definido este, obtenemos una estimación de una curva suave, que aproxima de forma óptima (con los mismos criterios que en estimación paramétrica) a una nube de puntos, como refleja la siguiente figura:
Un simple click en google buscando smoothing splines, nos lleva a wikipedia, que nos ofrece la definición en un lenguaje matemáticamente sencillo.
La primera referencia que vemos en wikipedia es el libro Spline Models for Observational Data (SIAM, 1990). No es casualidad y el lugar le hace justicia. La autora es Grace Wahba, un nombre imprescindible en cualquier relato de ese avance. Fue pionera en estos estudios y su libro, es ya un clásico, base de la investigación sobre el uso de splines y de las propuestas de nuevos estimadores con sus parámetros de suavizado asociados. Así, Grace Wahba es sobre todo conocida por el desarrollo del método generalizado de validación cruzada para la selección del parámetro de suavizado, método que encontramos implementado en los paquetes estadísticos habituales.
Sus aportaciones se enmarcan tanto en el análisis de propiedades estadísticas de nuevos estimadores, como en sus aplicaciones prácticas. Así, ha trabajado directamente en aplicaciones de sus técnicas a estudios demográficos, microanálisis de ADN, estudio de imágenes médicas o cambio climático, entre otros.
Grace Wahba se educó en Cornell (BA, 1956), y se doctoró en Stanford (1966), después de haber trabajado varios años en la empresa. Ha recibido numerosos reconocimientos por su trabajo. Así, fue elegida miembro de la United States National Academy of Sciences en 2000, recibió el doctorado de honor en Ciencia por la Universidad de Chicago en 2007 y fue nombrada estadística del año por la American Statistical Association en 2004. Ha dirigido más de una treintena de tesis doctorales, y se le asocian casi 200 descendientes científicos.
Su índice h de 60 nos da una idea cuantitativa de la repercusión de sus contribuciones. De entre ellas, las 4 más citadas han superado las 1000 citas (*). Desde luego, Grace Wahba sería merecedora, sin discusión, de un hipotético premio Nobel en estadística.
Coincidiendo con su 80 cumpleaños, la Universidad de Madison, a la que lleva vinculada desde 1967, celebrará en su honor el evento Conference on Nonparametric Statistics for Big Data el próximo mes de junio.
Tal y como se dice en el anuncio de la conferencia, su papel en el desarrollo de la teoría y práctica de la estadística no paramétrica para datos numerosos es fundamental. Mucho del trabajo en este campo se deriva directamente de sus contribuciones, y no hubiera sido posible sin su implicación y visión.
¡Felicidades y gracias, Grace!
(*) Fuente: Google Scholar
- Spline models for observational data, 1990, SIAM (5349 citas)
- Smoothing noisy dta with spline functions, 1978, con P. Craven. Numerische Mathematik 31 (4), 377-403 (2733 citas)
- Generalized cross-validation as a method for choosing a good ridge parameter, con G.H. Golub y M. Heath. Technometrics 21 (2), 215-223 (2045 citas)
- Some results on Tchebycheffian spline functions, con G. Kimeldorf, Journal of Mathematical Analysis and Applications 33 (1), 82-95 (1000 citas)
Sobre la autora
Eva Ferreira es licenciada en Matemáticas, doctora en Economía y profesora de Estadística en la UPV/EHU. Es investigadora de teoría de procesos estocásticos y aplicaciones, y realiza divulgación sobre las aplicaciones de modelos probabilísticos.