Los tiranos no pueden impedir que hagamos matemáticas. Al menos hay algo que no nos pueden quitar.
Profesora en la Cátedra de Teoría de Números en el Instituto de Matemáticas de la Escuela Politécnica Federal de Lausana (EPFL), Maryna Viazovska fue galardonada con la Medalla Fields en julio de 2022. Se premiaba su trabajo sobre el empaquetamiento de esferas: resolvió en 2016 el problema del empaquetamiento en dimensión 8 y, en colaboración con otros investigadores, en dimensión 24.
Nacida en Kiev el 2 de diciembre de 1984, Maryna Viazovska es la mayor de tres hermanas en una familia muy cercana a la ciencia: su madre es ingeniera y su padre, químico. Casada con el físico ucraniano Daniil Evtushinsky, el matrimonio tiene un hijo y una hija.
Maryna eligió las matemáticas desde pequeña, se le daban especialmente bien en la escuela. En una de las entrevistas concedidas tras recibir la Medalla Fields, comentaba que era rápida para las matemáticas, pero no tanto para la lengua, aunque le gustaba leer, especialmente libros de ciencia ficción.
En 1998 ingresó en el Liceo de Ciencias Naturales de Kiev no. 145, una institución de enseñanza secundaria especializada en matemáticas, física y computación. Su alumnado se selecciona entre personas destacadas, como Maryna, cuyo rendimiento en matemáticas era superior a la media. Tras graduarse en 2001, ingresó en la Universidad Nacional Taras Shevchenko de Kiev para estudiar matemáticas; allí obtuvo su licenciatura en 2005. Después viajó a Alemania para cursar una maestría en la Universidad Técnica de Kaiserslautern, graduándose en 2007. En mayo de 2010 defendió su tesis de Candidato de Ciencias en el Instituto de Matemáticas de la Academia Nacional de Ciencias de Ucrania.
Después de obtener este título, viajó al Instituto Max Planck de Matemáticas en la Universidad de Bonn, donde realizó la tesis doctoral bajo la supervisión del especialista en teoría de números Don Zagier (1951). Defendida en 2013, esta memoria trataba sobre funciones modulares.
Después de un tiempo como investigadora postdoctoral en el Institut des Hautes Études Scientifiques en Francia, en 2014 Viazovska se mudó a Berlín donde trabajó en la Escuela Matemática de Berlín y la Universidad Humboldt de Berlín.
En enero de 2018 consiguió la cátedra que actualmente ocupa en la EPFL.
El problema de empaquetamiento de esferas
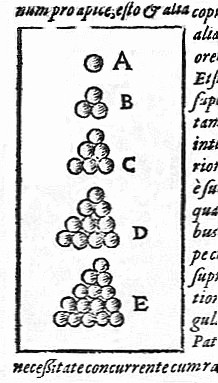
ilustrando la conjetura de Kepler.
Fuente: Wikimedia Commons.
La conjetura de Kepler fue enunciada por Johannes Kepler (1571-1630) en su ensayo Strena seu de nive sexangula de 1611. El astrónomo comenzó a interesarse por los ordenamientos de esferas gracias a su correspondencia con el matemático y astrónomo Thomas Harriot (1560-1621). El marino Walter Raleigh (1552-1618) había planteado a Harriot el problema de encontrar la mejor manera de amontonar balas de cañón en la cubierta de sus barcos. Y Harriot se lo comentó a Kepler, quien conjeturó que la manera óptima de apilarlas era mediante un arreglo piramidal de caras centradas.
En la primavera de 2016 Maryna Viazovska anunció que había conseguido resolver un caso particular del problema de empaquetamiento de esferas, que generaliza en cualquier dimensión la conjetura de Kepler. Lo explicaba de esta manera en una entrevista concedida en 2017:
La pregunta es: ¿cuántas bolas de ocho dimensiones caben en un espacio de ocho dimensiones? Es decir, ¿con qué densidad se pueden empaquetar allí? […] En dimensión tres, este es el famoso problema de Kepler formulado ya en 1611. Se resolvió a finales del siglo XX con ayuda de computadoras. Existen innumerables maneras de colocar bolas tridimensionales, incluso con un ordenador es imposible verificar todos los casos. Pero surgió la idea de reducirlo a un cierto cálculo finito, aunque todavía muy largo y complicado. Es una historia bastante dramática. Un matemático anunció la solución, pero luego encontró muchos errores en ella. A principios de la década de 1990, otro científico de China hizo una declaración similar, pero también se encontraron muchos fallos. Y solo Tom Hales, después de pasar varios años, señaló la respuesta correcta en 1998. Se ha prestado una meticulosa atención a este trabajo, se ha revisado durante mucho tiempo, se ha revisado por pares durante cinco años, y se ha debatido si debiera considerarse como una solución matemática porque depende en gran medida de cálculos informáticos. Pero decidieron que todo era correcto. Y, recientemente, Hales también escribió una solución formal que se puede probar usando un programa de ordenador que, de hecho, está diseñado para validar tal evidencia. […] Resulta que hay una especie de atajo en el espacio de ocho dimensiones, por lo que podemos ir por un camino más fácil. En 2003, hubo novedades que indicaban que esto podía probarse. Me las arreglé para terminar este argumento de una manera lógica. Luego, trabajando con colegas, resolvimos el problema en dimensión 24.
En el artículo The sphere packing problem in dimension 8 Viazovska demostraba que el empaquetamiento óptimo de esferas de dimensión 8 era una configuración del espacio de ocho dimensiones denominada retículo E8. Su prueba involucraba una determinada función que Viazovska construía de manera explícita utilizando técnicas de teoría de números (formas modulares y casimodulares) y de análisis de Fourier.
Poco tiempo más tarde, junto a sus colaboradores habituales y el matemático Henry Cohn, resolvió el problema en dimensión 24. En este caso, esa configuración especial es el denominado retículo de Leech, que permite colocar 196 560 esferas de dimensión 24 tangentes a una esfera central. Tras el largo proceso que llevó a Viazovska a resolver el caso en dimensión 8, Cohn se dio cuenta de que la ingeniosa estrategia usada por Maryna podía utilizarse también en dimensión 24: en pocos días, este segundo caso se solucionó.
La medalla Fields llega en 2022
La matemática iraní Maryam Mirzakhani (1977-2017) se convirtió en 2014 en la primera mujer en ganar la Medalla Fields, el prestigioso premio que otorga cada cuatro años la Unión Matemática Internacional (IMU) durante el Congreso Internacional de Matemáticos (ICM).
En 2018, Maryna Viazovska era una de las personas candidatas a recibirla, aunque tuvo que esperar otros cuatro años para que ese sueño se cumpliera. Es la segunda mujer que recibe este galardón; en los 86 años de existencia del premio, 62 hombres –aunque Grigori Perelman (1966) rehusó aceptarla en 2006– y dos mujeres han obtenido la Medalla Fields.
El gran mérito de Viazovska reside en haber sabido relacionar disciplinas muy distintas –el análisis de Fourier y la teoría de formas modulares– para descubrir “estructuras muy simples, naturales, profundas, cosas que nadie esperaba y que nadie más había podido encontrar”, como comentaba Henry Cohn en la laudatio que le dedicó durante el ICM para celebrar su trabajo.
La técnica descubierta por Viazovska para resolver el problema de empaquetamiento de esferas está estrechamente vinculada a las dimensiones 8 y 24. Para el resto de las dimensiones (mayores que 3) será necesario buscar nuevos métodos para encontrar esas configuraciones óptimas.
Como la propia Maryna Viazovska comenta, ella es una matemática teórica que desconoce la posible utilidad “práctica” (al margen de las matemáticas) de los objetos con los que trabaja. ¡Cuántas veces le habrán preguntado para qué sirven esas complejas estructuras que manipula!
El topólogo algebraico Jaume Aguadé escribía hace 30 años un hermoso artículo titulado Cien años de E8.; en él habla precisamente de las insólitas aplicaciones que poseen esas matemáticas que centran la investigación de Maryna Viazovska:
[…] ¿Para qué puede servir –se preguntará– empaquetar esferas de dimensión 8? Sirve para llamar por teléfono, para escuchar Mozart en un Compact Disc, para enviar un fax, para ver televisión vía satélite, para conectar, mediante un módem, con una red de ordenadores. Sirve en todos aquellos procesos en que se exija la transmisión eficiente de información digital. La teoría de la información nos enseña que los códigos de transmisión de señales son más fiables en dimensiones elevadas y el retículo de E8, con su sorprendente simetría y dada la existencia de un decodificador apropiado (Conway 1982), es un instrumento fundamental en la teoría de la codificación y transmisión de señales. […]
Referencias
- Página personal, EPFL
- Maryna Viazovska, The sphere packing problem in dimension 8, of Math. 185 (2017), no. 3, 991-1015
- Henry Cohn, Abhinav Kumar, Stephen D. Miller, Danylo Radchenko and Maryna Viazovska, The sphere packing problem in dimension 24. of Math. 185 (2017), no. 3,1017-1033
- Henry Cohn, The work of Maryna Viazovska, ICM 2022
- Davide Castelvecchi, Ukrainian mathematician becomes second woman to win prestigious Fields Medal, Nature607 (2022) 224-225
- Davide Castelvecchi, ‘Mathematics is an unknown land’: meet Fields Medal winner Maryna Viazovska, Nature607 (2022) 649
- Thomas Lin and Erica Klarreich, In Times of Scarcity, War and Peace, a Ukrainian Finds the Magic in Math, Quanta Magazine, 5 julio 2022
- Jaume Aguadé, Cien años de E8, La Vanguardia, 8 junio 1991
- O’Connor, John J.; Robertson, Edmund F., Maryna Viazovska, MacTutor History of Mathematics archive, University of St Andrews
- Francisco R. Villatoro, Medallas Fields 2022 para Maryna Viazovska, James Maynard, June Huh y Hugo Duminil-Copin, La ciencia de la mula Francis, 5 julio 2022
- Wikipedia, Maryna Viazovska
Sobre el artículo original
El artículo Maryna Viazovska, la matemática que empaqueta esferas se publicó en el blog Cuaderno de Cultura Científica el 31 de agosto de 2022.
Sobre la autora
Marta Macho Stadler es doctora en matemáticas, profesora del Departamento de Matemáticas de la UPV/EHU y colaboradora en ::ZTFNews y la Cátedra de Cultura Científica de la UPV/EHU.
1 comentario
[…] Maryna Viazovska. Empaquetamiento de esferas. Conjetura de Kepler. Medalla Fields. Teoría de números. Funciones modulares. Análisis de Fourier. […]