Sophie Germain (1776-1831)

Sophie Germain fue una matemática autodidacta. Nació en París en las últimas décadas del Siglo de las Luces. Los cambios políticos y sociales que se producían en Francia durante su niñez determinaron que, desde muy pequeña, considerara la Ciencia y especialmente las Matemáticas, como el estímulo intelectual que daba sentido y tranquilidad a su existencia.

Sus primeros trabajos en teoría de números los conocemos a través de su correspondencia con C. F. Gauss, con el que mantenía oculta su identidad bajo el pseudónimo de Monsieur Le Blanc. El teorema que lleva su nombre fue el resultado más importante, desde 1753 hasta 1840, para demostrar el último teorema de Fermat, además permitió demostrar la conjetura para n igual a 5. Posteriormente sus investigaciones se orientaron a la teoría de la elasticidad y, en 1816, consiguió el Premio Extraordinario de las Ciencias Matemáticas que la Academia de Ciencias de París otorgaba al mejor estudio que explicara mediante una teoría matemática el comportamiento de las superficies elásticas, y publicó varios libros sobre este tema. En los últimos años de su corta vida, además de dos trabajos matemáticos, uno sobre la curvatura de superficies y otro sobre teoría de números, escribió un ensayo sobre filosofía de la ciencia, que Auguste Comte citó y elogió en su obra.

La historia de Sophie es la de una matemática brillante que no pudo lograr su pleno desarrollo porque en sus años de formación no pudo acceder a una educación matemática formal, y en su madurez tuvo que trabajar en solitario porque una jerarquía científica, totalmente masculina, la excluía. Tener una formación autodidacta, anárquica y con lagunas le perjudicará toda su vida. Su aislamiento no fue tan evidente cuando trabajaba en teoría de números, pero cuando comenzó a trabajar en física matemática no tuvo, en un primer momento, los últimos conocimientos matemáticos que entonces se estaban utilizando y que requerían un trabajo cada vez menos solitario y ligado a la comunidad científica. Aunque su obra merecía el reconocimiento académico, nunca recibió título alguno. Una calle de París y un Liceo llevan su nombre, y una placa, en la casa donde murió, (el número 13 de la rue de Savoie) la recuerda como matemática y filósofa. Actualmente, el Instituto de Francia, a propuesta de la Academia de Ciencias, concede anualmente “Le prix Sophie Germain” al investigador que haya realizado el trabajo más importante en Matemáticas, pero todo este reconocimiento es póstumo, ya que incluso en su certificado de defunción lo que figura como profesión es rentista y no matemática.

Su vida

Marie-Sophie Germain nació el día 1 de abril de 1776, en la calle de Saint Denis de París. Fue la segunda hija del matrimonio entre Marie-Madelaine Gruguelin y Ambroise-François Germain, un burgués cultivado y liberal, que participó activamente en la Revolución francesa y fue elegido diputado de los Tiers-État en la Asamblea Constituyente de 1789.

A los 13 años, en plena Revolución, convencida de que su familia sólo pensaba en el dinero y la política, se refugió en la lectura comenzando con las obras de la biblioteca de su padre. Su interés por las matemáticas surgió después de leer la Historia de las Matemáticas de Jean-Baptiste Montucla. En particular le impresionó la leyenda de la muerte de Arquímedes, por los soldados romanos, mientras estaba absorto en un problema de geometría. Quedó tan conmovida por el fuerte efecto de la matemática, capaz de hacer olvidar la guerra, que decidió dedicarse a su estudio.

Leía todo lo que caía en sus manos con un ardor que preocupaba a su familia. El matemático italiano Guglielmo Libri [NI] que más tarde será su amigo, nos cuenta como superó los obstáculos que sus padres habían ideado para frenar su pasión hacia las matemáticas. Para que no pudiera estudiar a escondidas de noche, decidieron dejarla sin luz, sin calefacción y sin sus ropas. Sophie parecía dócil, pero sólo en las apariencias, de noche, mientras su familia dormía, se envolvía en mantas y estudiaba a la luz de una vela que previamente había ocultado. Un día la encontraron dormida sobre su escritorio, con la tinta congelada, delante de una hoja llena de cálculos. Su tenacidad venció la resistencia de sus padres que aunque no comprendían su dedicación a las matemáticas terminaron por dejarla libre para estudiar. Comenzó por el tratado de aritmética de Étienne Bezout y el de cálculo diferencial de A. J. Cousin para seguir, después de aprender latín sin ninguna ayuda, con las obras de Isaac Newton y Leonhard Euler.

Tenía 18 años en 1794, cuando se fundó la Escuela Politécnica de París. Como las mujeres no eran admitidas (la Escuela Politécnica no admitirá mujeres hasta 1972), consiguió hacerse con apuntes de algunos cursos, entre ellos, el de Análisis de Lagrange. Al final del período lectivo los estudiantes podían presentar sus investigaciones a los profesores, Sophie presentó un trabajo firmándolo como Antoine-Auguste Le Blanc, un antiguo alumno de la escuela. El trabajo impresionó a Joseph Louis Lagrange (1736-1813) por su originalidad y quiso conocer a su autor. Al saber su verdadera identidad, la felicitó personalmente y le predijo éxito como analista, animándola de esta forma a seguir estudiando.

En 1798, Adrien-Marie Legendre (1752-1833) había publicado Essai sur la théorie des nombres y en 1801, apareció el libro de Karl Friedrich Gauss (1777-1855) Disquisitiones Arithmeticae. Sophie, impresionada por estas obras, se dedicó al estudio de la teoría de números. Entre 1804 y 1809 escribió a Gauss una decena de cartas mostrándole sus investigaciones. Temerosa del ridículo que en aquella época suponía una mujer erudita, las primeras cartas estaban firmadas con el seudónimo Le Blanc. Pero esta correspondencia fue irregular, Gauss estaba tan ocupado en su propia investigación que sólo le contestaba cuando el trabajo de Sophie estaba relacionado con sus propios teoremas.

Con motivo de la conquista de Prusia por Napoleón, en la campaña de Jena (1806), temió por la vida de Gauss y se puso en contacto con un militar amigo de su familia, el general Pernetti, para pedirle que velara por su seguridad. El militar le comunicó que había contactado con Gauss y que éste agradecía su mediación, pero que afirmaba no conocer a Sophie Germain. En la siguiente carta que le escribió tuvo que revelarle la verdad: ella era M. Le Blanc. Gauss sorprendido al conocer su identidad, elogia su talento y su genio [NII]. En la última carta que, en esta época, escribió a Gauss, le comentaba un resultado muy importante sobre teoría de números, el teorema que hoy lleva su nombre, pero él no respondió a esa carta.

En 1808, el ingeniero alemán Ernst Chladni presentó en París sus experiencias sobre la vibración de las superficies elásticas observando las figuras formadas cuando se esparcía arena sobre una placa y se la hacía vibrar al puntear el borde con el arco de un violín. La arena se concentraba donde las vibraciones eran más débiles, formando figuras geométricas muy interesantes. Estas experiencias se realizaron delante de un grupo de élite de sesenta y seis personas que constituían la “Primera Clase” de matemáticos y físicos del Instituto de Francia, después se repitieron delante de Napoleón.

La Academia de Ciencias de París tenía la costumbre de ofrecer un premio al mejor trabajo en ciencias físicas y matemáticas. Se elegía una comisión de cuatro o cinco personas que planteaba un tema y se establecía un programa. Los candidatos tenían dos años para hacer la memoria que presentaban de forma anónima. En 1809 la cuestión que propuso la Academia fue obtener una teoría matemática sobre las superficies elásticas que explicara las experiencias de Ernst Chladni.

La convocatoria de este concurso, y el hecho de que Gauss ya no contestaba a sus cartas, propiciaron que Sophie abandonara la teoría de números y comenzara sus investigaciones en física-matemática. Tuvo que presentar tres memorias sucesivas en 1811, 1813 y 1815 hasta conseguir, el 8 de enero de 1816, el Prix Extraordinaire de la Academia de Ciencias. Se reunió mucha gente para ver a la famosa mujer matemática, pero Sophie no asistió a la ceremonia de entrega. Aunque años antes se había considerado una novata entre gigantes, en ese momento no sentía ninguna admiración por muchos de sus colegas. [6]

A partir de entonces consiguió el respeto y el reconocimiento por parte de la comunidad científica, debido, sobre todo, a su amistad con Jean-Baptiste Joseph Fourier (1768-1830) que, después de ser elegido Secretario Permanente de la Academia de Ciencias, le permitió asistir a sesiones, siendo la primera mujer, no esposa de académico, que lo hizo. También continuó sus investigaciones con Legendre sobre teoría de números con el que trabajaba en un plano de igualdad, y reanudó la correspondencia [NIII] con Gauss sobre este tema.

El 27 de junio de 1831 murió en París a consecuencia de un cáncer de pecho a los 55 años. A pesar de su extensa correspondencia, Gauss y Sophie nunca se conocieron personalmente. Gauss intentó que la Universidad de Gotinga le otorgara el título de doctor honoris causa; pero a pesar de su gran influencia en esta universidad, su propuesta no tuvo éxito. No será éste un hecho para recordar a Sophie Germain, pero siempre la evocaremos por su obra, que perdurara siempre, y por su talento que fue excepcional, además de otras cualidades como su valor y su dedicación a la ciencia.

Su obra

Sus primeros trabajos en teoría de números los conocemos a través de su correspondencia con Gauss. Entre 1804 y 1809 Sophie escribió a Gauss una decena de cartas en las que le comentaba sus investigaciones. Las primeras estaban firmadas con el pseudónimo Le Blanc. En 1819 se reanudó esta correspondencia.

En noviembre de 1804 está fechada la primera carta. Gauss, en su respuesta, admira la elegancia de una de sus demostraciones [NIV]. En 1808 comunicó a Gauss su más brillante descubrimiento en teoría de números. Demostraba que si x, y, z son números enteros, tales que x⁵+y⁵+z⁵=0, entonces, al menos uno de los números x, y o z debe ser divisible por 5. Más tarde generalizó este resultado en el teorema que hoy lleva su nombre.

El teorema de Germain [21] constituyó un paso importante para demostrar el último teorema de Fermat [20]. De hecho, a partir de entonces, la demostración se dividió en dos casos: el primero consistía en probarlo cuando ninguno de los números x, y, z es divisible por n, y el segundo cuando uno sólo de los tres números es divisible por n. Además, con esta clasificación, el primer caso del teorema de Fermat para n=5 quedaba probado. En 1825 Legendre y Dirichlet completaron la demostración para n=5 en el segundo caso.

El teorema de Sophie Germain [16] demuestra que si n es un número primo tal que 2n+1 es primo, entonces el primer caso del teorema de Fermat es verdadero. El trabajo se había simplificado a la mitad. El teorema de Germain será el resultado más importante [NV] relacionado con la conjetura de Fermat desde 1738 hasta la obra de Ernst Eduard Kummer (1810-1893) en 1840. En teoría de números, se dice que un número natural es un número primo de Germain [17], si el número n es primo y 2n+1 también lo es. Los números primos de Sophie Germain [23] inferiores a 200, son: 2, 3, 5, 11, 23, 29, 41, 53, 83, 89, 113, 131, 173, 179 y 191.

Posteriormente, hacia 1819, Sophie retomó sus trabajos en teoría de números. De esta época es otro de los resultados de Sophie. Utilizando adecuadamente su teorema, conseguía demostrar que para todo número primo n menor que 100 (y por lo tanto para todo número menor que 100) no existe solución a la ecuación de Fermat, cuando los números x, y, z no son divisibles por n. Legendre seguirá su demostración para números primos n menores que 197.

Las investigaciones de Sophie, en teoría de números, sólo serán conocidas [NVI] porque Legendre las menciona en un artículo de 1823 que apareció en las Mémoires de l’Académie des Sciences en 1827, y en su Théorie des Nombres que se publicó en 1830. Una de las versiones más completas de su trabajo sobre la conjetura de Fermat es un manuscrito titulado “Observaciones sobre la imposibilidad de satisfacer la ecuación: xⁿ+yⁿ=zⁿ”, que se conserva en la Biblioteca Moreniana de Florencia [NVII].

Sus investigaciones en teoría de la elasticidad comienzan a partir de 1809 cuando la Academia de Ciencias de París propone como tema, para obtener el premio extraordinario de la Academia: “Donner la théorie mathématique des surfaces élastiques et la comparer à l’expérience”. Pierre Simon Laplace (1749-1827) que organizó este concurso, esperaba poder establecer la reputación de su protegido Siméon Denis Poisson (1781-1840) [NVIII]. Pero Poisson no participó.

Descubrir las ecuaciones diferenciales de las superficies vibrantes parecía demasiado difícil a los ojos de la mayor parte de los matemáticos. A pesar de las lagunas de su formación, o quizás por ello, Sophie fue la única concursante. Lo tomó como un reto, y el 21 de septiembre de 1811 presentó una memoria a la Academia, pero su trabajo fue considerado incompleto e incorrecto, y el jurado decidió posponer dos años más el premio. Lagrange corrigió el análisis matemático y obtuvo, a partir de la hipótesis de Sophie, la base para describir el comportamiento estático y dinámico de las placas en puntos del interior. De este trabajo sólo se conoce la ecuación final en una nota [NIX] de ocho líneas.

En esta memoria, y por analogía con los trabajos de Euler en el caso unidimensional de la cuerda vibrante, Sophie postula que “en un punto de la superficie la fuerza de elasticidad es proporcional a la suma de las curvaturas principales de la superficie en dicho punto”, que es lo que siempre llamará mi hipótesis. A partir de una supuesta relación de equilibrio, y utilizando varias hipótesis sobre los desplazamientos y rotaciones de la placa, obtenía una ecuación en derivadas parciales de sexto orden en la que buscaba soluciones regulares, en casos particulares, mediante series trigonométricas.

Aunque, en efecto, varios puntos de su trabajo son discutibles, la idea de que la suma de las curvaturas principales en una superficie tiene el mismo papel que la curvatura en el caso unidimensional de la cuerda vibrante es original. Además Sophie no se desalentó sino que, animada de que Lagrange hubiera utilizado con éxito su idea, siguió trabajando con el objetivo de justificar su hipótesis, con consideraciones geométricas sobre la deformación de un plano y comparando sus cálculos con las experiencias de Chladni y con otras muchas que realizó ella misma. En 1813 presentó la segunda memoria, por la que obtuvo una mención de honor ya que sus deducciones teóricas explicaban los resultados experimentales.

En 1814 Poisson redactó un trabajo sobre el mismo asunto que leyó el día 1 de agosto de ese mismo año, ante los componentes de la Primera Clase del Instituto de Francia, de la que formaba parte. Comenzó criticando el enfoque de los trabajos anteriores sobre este tema de Leonhard Euler, Jacques Bernouilli y, por último, de la memoria anónima que el año anterior había recibido una mención de honor. Poisson era discípulo de Laplace, y compartía con él la teoría “molecular” que intentaba explicar todos los fenómenos físicos con el modelo de la física newtoniana, es decir, por un conjunto de fuerzas atractivas o repulsivas. Desde este punto de vista, considerando el equilibrio de una sola molécula de la superficie elástica, obtuvo una ecuación, horrible, no lineal y además falsa, que por simplificaciones “milagrosas” [NX] se convertía en la ecuación de la segunda memoria de Sophie que, en ese momento, había ganado credibilidad. No la publicó, supuestamente, para no influir en el concurso que había sido convocado de nuevo, pero apareció un resumen de la misma en el Bulletin de la Societé Philomatique y en la Correspondance de l’Ecole Polytecnique. Sophie, que no tuvo acceso a ella y sólo pudo leer dicho resumen, en un principio se desalentó pero, más tarde, saber que Poisson había llegado a la misma ecuación que ella, le animó a continuar sus investigaciones y presentó otro estudio en 1815.

Este tercer trabajo: Mémoire sur les Vibrations des Surfaces Élastiques, por el que se le concedió, al fin, el premio extraordinario de la Academia, suponía una defensa de la legitimidad de su hipótesis a la vez que un ataque al modelo laplaciano y a la teoría molecular. También, en ella, se proponía matematizar el concepto de forma de una superficie y el de deformación. Planteaba que, considerando en un punto dado, la suma de las curvaturas relativas a todas las curvas producidas por las diferentes secciones de la superficie que pasan por la normal se obtendría una expresión que matematizaba la forma de la superficie en un punto. Por lo tanto estaba proponiendo, implícitamente, un procedimiento integral para definir la curvatura en el espacio… Además establecía que esta suma infinita se reducía a las dos curvaturas principales, es decir, las curvaturas máxima y mínima [4].

En 1821 la publicó, por cuenta propia, con el título Recherches sur la théorie des surfaces élastiques [8] posiblemente con objeto de pasar a la posteridad, que ningún colega se apropiara de sus investigaciones, o a causa de su rivalidad [NXI] con Poisson, que en su trabajo de 1814 había utilizado los resultados de su segunda memoria.

En 1826 publicó Remarques… [9] y en 1828 Examen des Principes… [10]. En estas dos memorias sus objetivos son, además de una intervención implícita en la polémica [NXII] suscitada entre Poisson y Navier sobre la teoría de la elasticidad, replantear su trabajo y, sobre todo, su enfoque, radicalmente opuesto al paradigma molecular y en particular al de Poisson.

Durante los sucesos revolucionarios que tuvieron lugar en París en julio de 1830, Sophie volvió a refugiarse en el estudio. Redactó dos trabajos, uno sobre teoría de números “Notes sur la manière dont se composent les valeurs de y et z dans la équation…” y otro sobre elasticidad en el que buscaba definir una teoría dinámica de la curvatura: “Mémoire sur la courbure des surfaces” donde introdujo el concepto de curvatura media como la semisuma de las curvaturas principales. Estas dos memorias fueron publicadas en 1831, después de su muerte, en la Revista Crelle. Una vez más su camino se cruzó con el de Gauss que acababa de publicar una teoría matemática de la curvatura en la que definía lo que hoy se conoce por curvatura gaussiana como el producto de las curvaturas principales.

Además de trabajar en matemáticas y física, Sophie se interesaba por la filosofía, química, historia y geografía. Su ensayo filosófico Considérations générales sur l’état des Sciences y des Lettres aux différentes époques de leur culture [11] fue publicado en 1833, después de su muerte. Una de sus ideas originales fue identificar los procesos intelectuales de las “Ciencias” y las “Letras” e incluso de todas las actividades humanas. Pero esta semejanza no es la parte más importante de la obra que pasa a un segundo plano frente a consideraciones mucho más profundas sobre el recorrido histórico, el carácter y la naturaleza de la ciencia. El concepto clave que unifica el texto es la “analogía” que permite ordenar y encontrar las leyes del universo. Esta obra fue elogiada por Auguste Comte en su Cours de philosophie positive y por Félix Ravaisson en su Rapport sur la philosophie en France au XIX siècle.

En 1824 había presentado a la Academia una memoria. Poisson, Laplace y el barón de Prony eran los encargados de evaluarla. Dicho informe no se hizo nunca. La Mémoire sur l’emploi de l’épaisseur dans la théorie des surfaces élastiques permaneció entre las posesiones de Prony. Cuando en 1879 se publicó Sophie Germain: Oeuvres philosophiques [NXIII] [11] se despertó de nuevo el interés por esta mujer y se recuperó dicha memoria que fue publicada en 1880 [2].

Bibliografía

[1] Alic, M. (1991): El legado de Hipatia. Historia de las mujeres desde la Antigüedad hasta fines del siglo XIX. Siglo veintiuno editores, Madrid, pp 176-185

[2] Bucciarelli, L. L., Dworsky, N. (1980): Sophie Germain. An essay in the History of the theory of Elasticity. Reidel Publishing Company, Dordrecht

[3] Dahan-Dammedico, A. (2000): Sophie Germain en “Les mathématiciens”. Belin, París, pp 72-85

[4] Dahan-Dammedico, A. (1988): Étude des méthodes et des styles de mathématisation: la science et l’élasticité en “Sciences à l’époque de la Révolution Française”. R. Rashed (ed). Blanchard, París, pp 349-442

[5] Dubreil-Jacotin, M. L. (1948): Figures de Mathématiciennes en “Les grands courants de la pensée mathématique”, F. Le Lionnais (ed.). Cahiers du sud, París, pp 260-261

[6] Figueiras, L.; Molero, M.; Salvador, A.; Zuasti, N. (1998): Género y Matemáticas. Editorial Síntesis, Madrid, pp 144-151

[7] Figueiras, L.; Molero, M.; Salvador, A.; Zuasti, N. (1998): El juego de Ada. Matemáticas en las Matemáticas. Proyecto Sur de Ediciones, S. L, Granada, pp 95-105

[8] Germain, S. (1821): Recherches sur la théorie des surfaces élastiques, Veuve Courcier, París

[9] Germain, S. (1826): Remarques sur la nature, les bornes et l´étendue de la question des surfaces élastiques et Équation Générale de ces Surfaces, Huzard Courcier, París

[10] Germain, S. (1828): Examen des principes qui peuvent conduire à la connaissance des lois de l’équilibre et du mouvement des solides élastiques, Annales de Chimie et de Physique, Tome XXXVII, pp 337.

[11] Germain, S (1879): Oeuvres philosophiques de Sophie Germain. H Stupuy (ed.) Paul Ritti, París (segunda ed. 1890)

[12] Got, T. (1948): Le dernier Théorème de Fermat en “Les grands courants de la pensée mathématique”, F. Le Lionnais (ed.), Cahiers du sud, París, 90-98

[13] Gray, M. W. (1987): Sophie Germain en “Women of Mathematics. A Biobibliographic Sourcebook”, L. S. Grinstein and P. J. Campbell, (ed), Greenwood Press, Connecticut

[14] Molero, M. y Salvador, A. (2004): Sophie Germain, Ed. Orto. Madrid

[15] Osen, L. M. (1992): Women in Mathematics. The MIT Press, Cambridge

En la web

[16] Radoux, C (1996): Quelques mathématiciennes, “Cahiers Rationalistes”, 501 y 502

[17] Caldwell, C. K. The Top Twenty: Sophie Germain Primes,

[18] Del Centina, A.: Letters of Sophie Germain preserved in Florence

[19] O’Connor, J. J.; Robertson, E. F: Marie-Sophie Germain

[20] O’Connor, J. J.; Robertson, E. F (1996): Fermat’s last theorem

[21] Riddle, L. (2001): Sophie Germain and Fermat’s Last Theorem

[22] Singh, S.; Nova web site on its production of “The Proof”

[23] Weisstein, E. W.: Sophie Germain Prime

Notas

[NI] La amistad entre Germain y Libri: Guglielmo Libri, Conde de Bagnano, nació en Florencia en 1802. Tuvo una educación excelente, inspirada por las nuevas ideas ilustradas y cultivadas de su familia. Comenzó sus estudios en la Universidad de Pisa a la edad de catorce años y en 1823 fue profesor de física y matemáticas en Pisa. Aunque Libri es mejor conocido como historiador de matemática, bibliófilo, gran coleccionista y comerciante de libros, produjo algunos teoremas, sobre todo en teoría de números, que todavía se citan, por ejemplo en 1832 había conjeturado que para un número primo n dado, sólo puede haber un número finito de primos de la forma kn+1 que satisfacen las dos condiciones del teorema de Sophie Germain. En 1876, A. E. Pellet demostró que la conjetura de Libri era correcta.

En 1819 Guglielmo Libri, a la edad de diecisiete años, oyó hablar de un premio de la Academia francesa por la demostración del Último Teorema de Fermat, y comenzó su investigación en este tema, estudiando ávidamente los trabajos de Euler, Legendre y Gauss. Su primer trabajo en teoría de números fue su Memoria sopra la teoria dei numeri, que publicó en Florencia en 1820. Libri tradujo su trabajo a francés y se lo envió a Cauchy para que lo presentara en la Academia de Ciencias de París. La memoria de Libri se recibió el 22 de enero de 1821 y Cauchy realizó una presentación verbal. Sophie Germain estudió esta memoria de Libri, de hecho, en la biblioteca Moreniana se conserva un manuscrito de tres páginas con el título Notes sur Memoria sopra la teoria dei numeri. En mayo de 1821, Libri envió a Cauchy otro trabajo en teoría de números para que lo leyera en la Academia. De modo que cuando Libri fue a París, tres años después, la comunidad científica lo recibió como a un joven matemático de mucho talento. Mientras vivía Sophie, Libri estuvo en París dos veces, la primera estancia duró desde finales de diciembre de 1824 hasta mitad de agosto de 1825, la segunda de primeros de junio a finales de julio de 1830.

Sophie Germain y Libri se encontraron por primera vez el 13 de mayo de 1825, en una de las reuniones que organizaba F. Arago los jueves por la tarde en el Observatorio de París. Al día siguiente, Libri, en una carta le comentaba a su madre: “finalmente anoche me encontré con Mademoiselle Germain, que ganó el premio extraordinario de matemáticas en el Instituto hace algunos años, hablé con ella dos horas, tiene una personalidad impresionante”. Parece que disfrutaron inmediatamente de su compañía y en la biblioteca Moreriana de Florencia se conservan varias cartas en las que Sophie invitaba a Libri a comer en su casa. En una de ellas invita también a L. Crelle (fundador de la Revista Crelle) que en el verano de 1830 estaba en París en visita oficial, por encargo del Ministerio de Educación de Prusia, para estudiar los métodos de enseñanza de las Matemáticas en Francia.

En septiembre de 1826 Sophie le escribió una carta en la que le comentaba la poca influencia que tenía en la comunidad científica, ante la ayuda que Libri le había pedido para obtener un puesto en la Academia de Ciencias. Durante más de tres años su correspondencia se suspende o está perdida. No se conoce ninguna carta entre ellos hasta febrero de 1830 cuando Sophie ya estaba muy enferma. Después de su muerte, Libri recibió de sus herederos muchos de sus manuscritos, parte de ellos se conservan en la biblioteca de Florencia, y en 1832 escribió una corta pero apasionada biografía de Sophie que apareció en una de las publicaciones del Instituto de Francia, el Journal de Débats.

[NII] Gauss elogia su talento en la carta fechada el 30 de abril de 1807 [11]: ^«Como describir mi admiración y mi asombro al ver a mi estimado M. Leblanc transformarse en este ilustre personaje que supone un ejemplo tan brillante que no habría podido creerlo. El gusto por las ciencias abstractas en general, y sobre todo por los misterios de los números, es muy raro, esto no es sorprendente, puesto que los encantos de esta sublime ciencia en toda su belleza sólo se revelan a aquellos que tienen el valor de profundizar en ella. Pero una mujer, debido a su sexo, a nuestras costumbres y prejuicios, encuentra infinitamente más obstáculos que un hombre para familiarizarse con esos complejos problemas y si a pesar de ello consigue superar estas trabas y penetrar en lo que está más oculto, indudablemente posee una valentía notable, un talento extraordinario y un genio superior. En efecto nada podría probar, de una manera más halagadora y menos equívoca, que los atractivos de esta ciencia, que han embellecido mi vida de tantas alegrías, no son quimeras, como la predilección con la que usted la ha honrado. Las sabias observaciones de las que vuestras cartas están tan ricamente repletas, me han proporcionado mil placeres. Las he estudiado con atención y admiro la facilidad con la que usted penetra en todas las ramas de la Aritmética y la sagacidad con la que obtiene su generalización y su perfección».

[NIII] Carta de Sophie a Gauss en mayo de 1819: «Aunque he trabajado durante algún tiempo en la teoría de superficies elásticas (a lo que tengo mucho que agregar si tuviera la satisfacción de realizar algunos experimentos en superficies cilíndricas que tengo en mente), nunca he dejado de pensar en la teoría de números… Hace tiempo que nuestra Academia propuso como materia para un premio la demostración de la imposibilidad de la ecuación de Fermat, este desafío me ha atormentado a menudo».

[NIV] Gauss admira la elegancia de la demostración. Respuesta de Gauss a la primera carta de Sophie en 1804: «Me complace comprobar su habilidad para la aritmética. Sobre todo su nueva demostración para números primos, cuando 2 es o no es residuo cuadrático, me ha gustado mucho, es una demostración muy aguda, es una pena que no se pueda aplicar a otros números…».

[NV] A. Dahan Dalmedico, «Sophie Germain», 2000 [3]: «Desde 1753, fecha de la carta de Euler a Goldbach diciendo que había conseguido demostrar el teorema de Fermat para n igual a 3, hasta los trabajos de Kummer en 1840, el teorema de Germain es el resultado más importante relacionado con el teorema de Fermat». Hoy conocemos que la demostración de Euler tenía un error que podría corregirse utilizando sus propios resultados. También Gauss demostró que la ecuación de Fermat no tenía solución para n=3, pero su demostración no fue publicada hasta después de su muerte.

[NVI] T. Got. «Le dernier Théorème de Fermat», 1943 [12]: «Es en su gran memoria de 1823 sobre el teorema de Fermat cuando Legendre da a conocer el siguiente teorema muy importante que le había sido comunicado por una matemática de gran talento, Sophie Germain. Si n es primo y 2n+1 es primo o de forma general 2kn+1 es primo, para el que no existen dos restos de potencias enésimas que sean consecutivos, la ecuación de Fermat no es posible si ninguno de los números x, y, z es divisible por n».

[NVII] En la Biblioteca Moreniana de Florencia [18] en los fondos del matemático G. Libri, se han preservado muchos manuscritos de Sophie Germain, más de doscientas hojas sobre: trabajos científicos, notas sobre experimentos, proyectos de cartas a Gauss, Legendre, Lagrange, notas sobre los artículos de Cauchy y Navier sobre elasticidad (entre estos documentos se encuentra el manuscrito citado)…. Después de la muerte de Sophie, G. Libri recibió de sus herederos gran parte de los manuscritos que ella tenía. Algunos de ellos, entre los que estaban varias cartas de Gauss, se vendieron al Príncipe B. Boncompagni. Otro material se ha dispersado y probablemente perdido para siempre. Actualmente muchos de sus manuscritos se encuentran en la Biblioteca Nacional de Francia.

[NVIII] Poisson nació en 1781 y comenzó sus estudios en la Escuela Politécnica en 1789; fue un espíritu abstracto y un brillante calculador. Realizó una carrera muy fácil gracias al apoyo de Laplace. Fue profesor de la Facultad de Ciencias de París y de la Escuela Politécnica, además en 1812 fue elegido miembro de la Academia de Ciencias. Frecuentaba asiduamente la famosa Sociedad de Arcueil, formada por los partidarios de las ideas de Laplace, sus reuniones eran un centro de discusión, comunicación y realización de experiencias, dirigidas por Laplace, Berthollet y Poisson.

[NIX] Nota de Lagrange sobre la ecuación de la placa a partir de la primera memoria de Sophie (Annales de Chimie et de Physique. Tomo 39, página 149). «La ecuación fundamental para el movimiento de la superficie vibrante no me parece exacta, así como la manera de encontrarla al deducirla de la de una lama elástica, el paso de una línea a una superficie me parece poco justificado.
Cuando los z son muy pequeños la ecuación se reduce a:

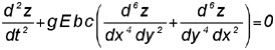
Pero adoptando como el autor (1/r+1/r’) como medida de la curvatura de la superficie, que la elasticidad tiende a disminuir y a la cual se la supone proporcional, la ecuación que he encontrado para el caso de z muy pequeño sería la siguiente.

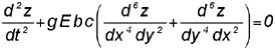
que es bien diferente».

[NX] Bucciarelli, L. L., Dworsky, N. [2]: «Parece un milagro que esta ecuación conduzca por simplificaciones adecuadas de linealización a la ecuación del movimiento de la placa vibrante encontrada por Lagrange y por Sophie Germain en su segunda memoria».

[NXI] La rivalidad entre Sophie Germain y Poisson comenzó con la lectura que éste realizó en 1814, ante los miembros de la Academia, de su memoria sobre elasticidad, trabajo que no hizo público, pero que dio a conocer su existencia y sus conclusiones, y en el que utilizaba los resultados de las dos primeras memorias de Sophie. Mientras tanto ella realizaba su tercer trabajo,que además iba a ser juzgado por Poisson, pues había sido elegido para formar parte del jurado. Además cuando recibió el premio extraordinario de la Academia en 1816, el jurado había admitido ciertas reservas sobre sus demostraciones, por lo que Sophie escribió a Poisson resumiendo en nueve enunciados las hipótesis físicas en las que se basaba su memoria.

Carta de Germain a Poisson: «No creo haberme equivocado en la forma de deducir la ecuación general de mi hipótesis, por lo tanto debe ser mi hipótesis la que no está justificada de manera satisfactoria. Para evitaros recibir toda la demostración he reproducido en la nota adjunta los razonamientos sobre los que está fundamentada. Están escritos de forma separada para que os sea fácil determinar el lugar en el que usted juzga que la cadena de razonamientos está interrumpida. (Cadena de razonamientos):

• Todas las fuerzas que podamos considerar son proporcionales al efecto que producen o tienden a producir.
• Las fuerzas de la elasticidad tienden a eliminar la diferencia entre la forma natural de los cuerpos debidas a ellos mismos y la forma que los mismos cuerpos se ven forzados a tomar por el efecto de una causa exterior.
• Las fuerzas de la elasticidad que actúan sobre cualquier cuerpo elástico se pueden medir con la diferencia entre la forma natural de ese cuerpo y la forma que toman bajo el efecto de una causa exterior.
• El efecto producido por una fuerza es, explícitamente o implícitamente, el conjunto de los efectos producidos por la misma fuerza.
• Explícitamente si se consideran sucesivamente todos los efectos sin expresar que unos dependen de los otros; implícitamente si la relación que existe entre los mismos efectos permite considerarlos como un efecto único.
• El efecto de las fuerzas de elasticidad que actúan sobre una superficie es eliminar la diferencia entre la curvatura natural de la superficie y la curvatura que ha sido forzada a tomar por el efecto de una fuerza exterior, pero la pregunta sobre la curvatura de una superficie no es susceptible de una respuesta simple; está compuesta de un conjunto de preguntas relativas a la curvatura de las curvas resultantes de las secciones de la misma superficie hechas en todas las direcciones y según todas las inclinaciones posibles.
• El conjunto de las diferencias entre las curvaturas de las distintas secciones de la superficie, consideradas antes y después de la acción de la causa exterior, es explícitamente la medida de las fuerzas de elasticidad que actúan sobre esa superficie.
• Existe entre las curvaturas de las curvas formadas por las distintas secciones de la superficie una relación tal que podemos expresar sus sumas por las de las secciones principales.
• El efecto de las fuerzas de elasticidad está pues implícitamente expresado por la suma de las únicas diferencias entre las curvaturas principales de la superficie, consideradas antes y después de la fuerza exterior».

La respuesta de Poisson [11] a esta carta fue lacónica y formalmente cortés, se limitó a enviarle su propia memoria. Pero evitó toda discusión seria con ella sobre cuestiones de fondo y públicamente fingía ignorarla.

También las dos memorias de Fourier sobre la teoría del calor de 1807 y 1810 habían sido leídas por Lagrange, Laplace, Poisson y criticadas por su falta de hipótesis física sobre la naturaleza del calor, pero mientras que Fourier pudo defender sus planteamientos, Sophie nunca tuvo un interlocutor intelectual y científico para sus teorías sobre la elasticidad a pesar de que sus desarrollos matemáticos no convencían a algunos miembros de la Academia.