María Barbero, profesora ayudante doctor en la Universidad Politécnica de Madrid y miembro del ICMAT
Campo de trabajo: Teoría de control
Problema en el que trabaja: construcción de integradores geométricos
¿Por qué nuestro cuerpo se mueve como lo hace? ¿Por qué ponemos en funcionamiento las articulaciones del brazo de una cierta manera para comer? Sin saberlo estamos resolviendo un problema de optimización cada vez que nos movemos. El objetivo a minimizar habitualmente es el tiempo, la distancia, la energía. Detrás de estos procesos y muchos otros de nuestro alrededor se esconde la teoría de control. Hoy en día la teoría de control se emplea en numerosos campos, como en medicina, aeronáutica, robótica, economía, etc. Entre sus aplicaciones, está el diseño de coches autodirigidos, de velas solares, etc.
Para su desarrollo hacen falta matemáticas avanzadas que derivan de la mecánica, es decir, del análisis del movimiento de los cuerpos y su evolución en el tiempo bajo la acción de fuerzas. La teoría de control estudia sistemas dinámicos en los cuales podemos intervenir debido a los grados de libertad que añaden los controles al sistema. Por ejemplo, cada vez que nos sentamos al volante de un coche estamos manejando un sistema de control (pisamos los pedales, giramos el volante y cambiamos de marcha). Estos controles están a nuestra disposición para conducir correctamente y llegar sanos y salvo a nuestro destino. Nuestras elecciones y las de los conductores a nuestro alrededor permitirán un viaje seguro.
El comportamiento del sistema se puede definir según los valores de los controles admisibles, los campos de control y la deriva propia del sistema. Un modelo simplificado de un coche viene descrito por las ecuaciones diferenciales
![]() donde u es el control sobre la velocidad angular del giro del volante que toma valores en el intervalo [-1,1]. Este vehículo se mueve a velocidad lineal constante. Existen modelos más complicados que permiten modificar la velocidad lineal y el cambio de marchas. Hay tantos campos de control como controles tiene el sistema. Los campos de control son campos vectoriales que corresponden a los términos con controles, en este caso es simplemente ∂/∂θ. La deriva propia del sistema es el movimiento libre del coche, es decir, cuando el control se mantiene a cero. En este caso en un mundo sin fricciones el coche avanzará a velocidad constante a lo largo línea recta determinada por el valor inicial del ángulo θ.
donde u es el control sobre la velocidad angular del giro del volante que toma valores en el intervalo [-1,1]. Este vehículo se mueve a velocidad lineal constante. Existen modelos más complicados que permiten modificar la velocidad lineal y el cambio de marchas. Hay tantos campos de control como controles tiene el sistema. Los campos de control son campos vectoriales que corresponden a los términos con controles, en este caso es simplemente ∂/∂θ. La deriva propia del sistema es el movimiento libre del coche, es decir, cuando el control se mantiene a cero. En este caso en un mundo sin fricciones el coche avanzará a velocidad constante a lo largo línea recta determinada por el valor inicial del ángulo θ.
Los sistemas de control más estudiados son aquellos que son afines en los controles. Esto significa que el sistema de ecuaciones diferenciales está regido afínmente por los campos de control, es decir, es de la forma
son los campos de control, con los que interaccionamos en el sistema. Cuando los controles no intervienen, u=0 y por tanto la ecuación
![]() rige el movimiento libre. Una vez fijado el control y dada una condición inicial existe una única solución del sistema. Dependiendo del objetivo a alcanzar se escogerá un control u otro.
rige el movimiento libre. Una vez fijado el control y dada una condición inicial existe una única solución del sistema. Dependiendo del objetivo a alcanzar se escogerá un control u otro.
En su investigación, María Barbero estudia esta teoría desde un punto de vista geométrico, es decir, cuando las soluciones de los sistemas de ecuaciones diferenciales anteriores se entienden como curvas integrales de campos vectoriales dependientes de los controles. En concreto, la geometría simpléctica y presimpléctica permiten estudiar problemas de control óptimo intrínsecamente. Se espera que la geometría diferencial permita entender mejor el problema y así obtener mejores diseños y algoritmos para manejar robots, satélites, etc.
Esto es especialmente importante en la construcción de integradores geométricos. Las ecuaciones diferenciales suelen ser muy difíciles de resolver, en muchos casos es imposible obtener soluciones exactas, por lo que se emplean programas de software matemático para generar aproximaciones de las soluciones. Este tipo de herramientas es utilizado continuamente por ingenieros en misiones espaciales, diseño de robots, etc. Desde los años 90, de la mano de la escuela de Marsden, se sabe que la construcción de métodos para resolver ecuaciones diferenciales que preserven las propiedades geométricas propias de los sistemas genera mejores soluciones al compararlas con los métodos numéricos anteriores. Estos nuevos métodos reciben el nombre de integradores geométricos. Esto ha abierto un nuevo campo de investigación que busca integradores geométricos preservando distintas propiedades del sistema, como la energía. La obtención teórica de estos métodos permitirá construir nuevos métodos numéricos a implementar en programas matemáticos, lo cual tendrá un gran impacto en la ingeniería.
Nota
Este artículo es una colaboración del Instituto de Ciencias Matemáticas (ICMAT) con Mujeres con ciencia.
Una versión reducida del artículo She makes math: María Barbero ha aparecido en el Undécimo número del Boletín ICMAT.
Sobre la autora
Ágata Timón García-Longoria es Licenciada en Matemáticas por la UCM y Máster en Periodismo y Comunicación de la Ciencia, la Tecnología y el Medio Ambiente por la UC3M. Es responsable de comunicación y divulgación en el Instituto de Ciencias Matemáticas (CSIC-UAM-UC3M-UCM).

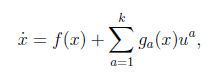
2 comentarios
cordial saludo.
Interes en opinar sobre algunas inquietudes de la fisica….
[…] 2) La serie She makes maths, sección habitual en el newsletter trimestral del ICMAT, aportando el retrato de una mujer matemática en su lugar de trabajo, y explicando su investigación. El perfil se extenderá en el Blog Mujeres con […]